备考2020年高考数学一轮复习:43 立体几何中的向量方法(一)--证明平行与垂直(理科专用)
试卷更新日期:2019-10-31 类型:一轮复习
一、单选题
-
1. 设直线 的方向向量为 ,平面 的法向量为 , ,则使 成立的是( )A、
 ,
,  B、
B、 ,
, 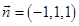 C、
C、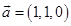 ,
,  D、
D、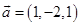 ,
, 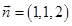 2. 已知A、B、C三点的坐标分别为 , , ,若 ,则 等于( )A、28 B、-28 C、14 D、-143. 下列选项中,与向量 垂直的单位向量为( )A、 B、 C、 D、4. 与向量 =(12,5)平行的单位向量为( )A、 B、 C、 或 D、 或5. 下列各组向量中不平行的是( )A、 B、 C、 D、6. 设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )A、2 B、-4 C、4 D、-27. 已知向量 , ,且 ,则 ( )A、 B、 C、 D、8. 若直线 的一个方向向量 ,平面 的一个法向量为 ,则( )A、 B、 C、 D、 都有可能9. 已知平面 的法向量是 ,平面 的法向量是 ,若 ,则 的值是( )A、 B、 C、6 D、
2. 已知A、B、C三点的坐标分别为 , , ,若 ,则 等于( )A、28 B、-28 C、14 D、-143. 下列选项中,与向量 垂直的单位向量为( )A、 B、 C、 D、4. 与向量 =(12,5)平行的单位向量为( )A、 B、 C、 或 D、 或5. 下列各组向量中不平行的是( )A、 B、 C、 D、6. 设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )A、2 B、-4 C、4 D、-27. 已知向量 , ,且 ,则 ( )A、 B、 C、 D、8. 若直线 的一个方向向量 ,平面 的一个法向量为 ,则( )A、 B、 C、 D、 都有可能9. 已知平面 的法向量是 ,平面 的法向量是 ,若 ,则 的值是( )A、 B、 C、6 D、二、填空题
-
10. 已知直线 的方向向量为 ,平面 的法向量为 ,若 ,则实数 的值为.11. 已知向量 ,若 ,则x=;若 则x= .12. 平面α与平面β垂直,平面α与平面β的法向量分别为=(﹣1,0,5),=(t,5,1),则t的值为13. 设平面α与向量=垂直,平面β与向量=垂直,则平面α与β位置关系是14. 设平面 的法向量为 ,平面 的法向量为 ,若 ∥ ,则 的值为
三、解答题



