备考2020年高考数学一轮复习:40 直线、平面平行的判定及其性质
试卷更新日期:2019-10-31 类型:一轮复习
一、单选题
-
1. 若平面α//平面β,直线 m⊂α ,n⊂β,则关于直线m、n的位置关系的说法正确的是( )A、m∥n B、m、n异面 C、m⊥n D、m、n没有公共点2. 平面a与平面β平行的条件可以是( )A、a内有无穷多条直线都与β平行 B、直线a∥a,a∥B,且直线a不在a内,也不在β内 C、直线a a,直线b B,且a∥B,b∥a D、a内的任何直线都与β平行3. 在三棱锥P-ABC中,E为线段AB(不包括端点)上一点,则错误的是( )A、一定存在唯一的平面a经过点E,使得平面a∥平面PAC B、一定存在唯一的平面a经过点E,使得平面a⊥平面PAC C、一定存在唯一的平面a经过点E,使得平面a⊥PA D、在平面ABC内,一定存在唯一的直线l经过点E,使得l∥平面PAC4. 如图,L、M、N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是( )
 A、垂直 B、相交不垂直 C、平行 D、重合5. 已知 是不重合的直线, 是不重合的平面,有下列命题:
A、垂直 B、相交不垂直 C、平行 D、重合5. 已知 是不重合的直线, 是不重合的平面,有下列命题:①若 ,则 ;②若 ,则 ;③若 ,则 且 ;④若 ,则 .
其中真命题的个数是( )
A、0 B、1 C、2 D、36. 在下列条件中,可判定平面 与平面 平行的是( )A、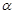 , β 都平行于直线 a
B、
, β 都平行于直线 a
B、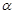 内存不共线的三点到 β 的距离相等
C、l ,
内存不共线的三点到 β 的距离相等
C、l ,  是
是 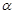 内的两条直线,且
内的两条直线,且  ,
,  D、l ,
D、l ,  是两条异面直线,且
是两条异面直线,且  ,
,  ,
,  ,
,  7. 下列四面体中,直线EF与MN可能平行的是( )A、
7. 下列四面体中,直线EF与MN可能平行的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,空间四边形ABCD中,E,F分别是AB,AD的中点,则EF与平面BCD的位置关系是( )
8. 如图,空间四边形ABCD中,E,F分别是AB,AD的中点,则EF与平面BCD的位置关系是( ) A、相交 B、平行 C、在平面内 D、不能确定9. 如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )
A、相交 B、平行 C、在平面内 D、不能确定9. 如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( ) A、MN∥PD B、MN∥PA C、MN∥AD D、以上均有可能10. 下列四个命题中,正确的是( )
A、MN∥PD B、MN∥PA C、MN∥AD D、以上均有可能10. 下列四个命题中,正确的是( )①夹在两条平行线间的平行线段相等;②夹在两条平行线间的相等线段平行;③如果一条直线和一个平面平行,那么夹在这条直线和平面间的平行线段相等;④如果一条直线和一个平面平行,那么夹在 这条直线和平面间的相等线段平行
A、①③ B、①② C、②③ D、③④11. 平面α与△ABC的两边AB,AC分别交于点D,E,且AD︰DB=AE︰EC,如图,则BC与α的位置关系是( ) A、平行 B、相交 C、平行或相交 D、异面12. 下列说法中正确的个数是( )
A、平行 B、相交 C、平行或相交 D、异面12. 下列说法中正确的个数是( )①平面α与平面β , γ都相交,则这三个平面有2条或3条交线;②如果a , b是两条直线,a∥b , 那么a平行于经过b的任何一个平面;③直线a不平行于平面α , 则a不平行于α内任何一条直线;④如果α∥β , a∥α , 那么a∥β.
A、0个 B、1个 C、2个 D、3个二、填空题
-
13. 下列四个正方体图形中, , 为正方体的两个顶点, , , 分别为其所在的棱的中点,能得出 平面 的图形的序号是
 14. α、β是两个平面,m、n是两条直线,有下列四个命题:
14. α、β是两个平面,m、n是两条直线,有下列四个命题:①如果m⊥n , m⊥α , n∥β , 那么α⊥β. ②如果m⊥α , n∥α , 那么m⊥n. ③如果α∥β , m α , 那么m∥β. ④如果m∥n , α∥β , 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号)
15. 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.其中正确的有(把所有正确的序号都填上).
 16. 三棱锥S-ABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为.
16. 三棱锥S-ABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为.
三、解答题
-
17. 如图,四棱锥P-ABCD的底面为平行四边形,M为PC中点.
 (1)、求证:BA∥平面PCD;(2)、求证:AP∥平面MBD.18. 如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1 , A1C1的中点,
(1)、求证:BA∥平面PCD;(2)、求证:AP∥平面MBD.18. 如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1 , A1C1的中点,
求证:
(1)、GH∥面ABC(2)、平面EFA1∥平面BCHG.


