备考2020年高考数学一轮复习:39 空间点、直线、平面之间的位置关系
试卷更新日期:2019-10-31 类型:一轮复习
一、单选题
-
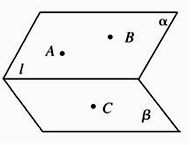
1. 已知平面 、 、 两两垂直,直线 、 、 满足: , , ,则直线 、 、 不可能满足以下哪种关系( )
A、两两垂直 B、两两平行 C、两两相交 D、两两异面2. 如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD , M是线段ED的中点,则( )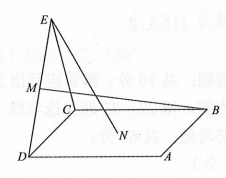 A、BM=EN , 且直线BM、EN 是相交直线 B、BM≠EN , 且直线BM , EN 是相交直线 C、BM=EN , 且直线BM、EN 是异面直线 D、BM≠EN , 且直线BM , EN 是异面直线3. 已知直线l是平面a的斜线,则a内不存在与l( )A、相交的直线 B、平行的直线 C、异面的直线 D、垂直的直线4. 下列命题中为真命题的是( )
A、BM=EN , 且直线BM、EN 是相交直线 B、BM≠EN , 且直线BM , EN 是相交直线 C、BM=EN , 且直线BM、EN 是异面直线 D、BM≠EN , 且直线BM , EN 是异面直线3. 已知直线l是平面a的斜线,则a内不存在与l( )A、相交的直线 B、平行的直线 C、异面的直线 D、垂直的直线4. 下列命题中为真命题的是( )①若 ,则 ; ②若 ,则 ;
③若 ,则 ; ④若 ,则 .
A、①② B、①②③ C、②③④ D、①②④5. 直三棱柱ABC—A1B1C1中,BB1中点为M,BC中点为N,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与MN所成角的余弦值为( )A、1 B、 C、 D、06. 如图,在正方体 中, 分别是棱 的中点,则异面直线 与 所成的角的大小是( )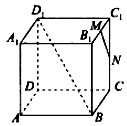 A、 B、 C、 D、7. 在正四棱锥 中, ,直线 与平面 所成的角为 , 为 的中点,则异面直线 与 所成角为( )A、 B、 C、 D、8. 如图,正四面体 中, 是棱 上的动点,设 ( ),记 与 所成角为 , 与 所成角为 ,则( )
A、 B、 C、 D、7. 在正四棱锥 中, ,直线 与平面 所成的角为 , 为 的中点,则异面直线 与 所成角为( )A、 B、 C、 D、8. 如图,正四面体 中, 是棱 上的动点,设 ( ),记 与 所成角为 , 与 所成角为 ,则( )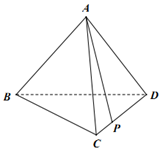 A、 B、 C、当 时, D、当 时,9. 设直线 与平面 平行,直线 在平面 上,那么( )A、直线 不平行于直线 B、直线 与直线 异面 C、直线 与直线 没有公共点 D、直线 与直线 不垂直10. 已知某四面体的六条棱长分别为3,3,2,2,2,2,则两条较长棱所在直线所成角的余弦值为( )A、0 B、 C、0或 D、以上都不对11. 已知 、 、 是三条不同的直线, 、 、 是三个不同的平面,则下列判断正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则12. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖膈,在鳖膈A-BCD中,AB⊥平面BCD,BC⊥CD,且AB=BC=CD,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )
A、 B、 C、当 时, D、当 时,9. 设直线 与平面 平行,直线 在平面 上,那么( )A、直线 不平行于直线 B、直线 与直线 异面 C、直线 与直线 没有公共点 D、直线 与直线 不垂直10. 已知某四面体的六条棱长分别为3,3,2,2,2,2,则两条较长棱所在直线所成角的余弦值为( )A、0 B、 C、0或 D、以上都不对11. 已知 、 、 是三条不同的直线, 、 、 是三个不同的平面,则下列判断正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则12. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖膈,在鳖膈A-BCD中,AB⊥平面BCD,BC⊥CD,且AB=BC=CD,M为AD的中点,则异面直线BM与CD夹角的余弦值为( )
A、 B、 C、 D、二、填空题
-
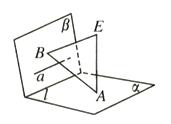
13. 如图所示,已知平面 平面 , ,垂足为 , ,垂足为 ,直线 , ,则直线 与直线 的位置关系是.
 14. 在正方体 中, 分别为棱 的中点,则异面直线 与 所成的角大小为 .15. 如图所示的几何体 中, 是平行四边形且 ,六个顶点任意两点连线能组成异面直线的对数是 .
14. 在正方体 中, 分别为棱 的中点,则异面直线 与 所成的角大小为 .15. 如图所示的几何体 中, 是平行四边形且 ,六个顶点任意两点连线能组成异面直线的对数是 .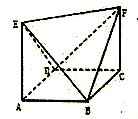 16. 已知直线l1:y=3x+1,l2:kx-2y-3=0,若l1∥l2 , 则k= .17. 若m,n表示直线,α表示平面,则下列命题中,正确命题的个数为 .
16. 已知直线l1:y=3x+1,l2:kx-2y-3=0,若l1∥l2 , 则k= .17. 若m,n表示直线,α表示平面,则下列命题中,正确命题的个数为 .① ⇒n⊥α;② ⇒m∥n;③ ⇒m⊥n;④ ⇒n⊥α.
三、解答题
-
18. A是 平面外的一点,E、F分别是BC、AD的中点,
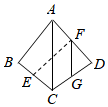 (1)、求证:直线EF与BD是异面直线;(2)、若 , ,求EF与BD所成的角.
(1)、求证:直线EF与BD是异面直线;(2)、若 , ,求EF与BD所成的角.