备考2020年高考数学一轮复习:38 空间几何体的表面积与体积
试卷更新日期:2019-10-31 类型:一轮复习
一、单选题
-
1. 祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高。若某柱体的三视图如图所示,则该柱体的体积是( )
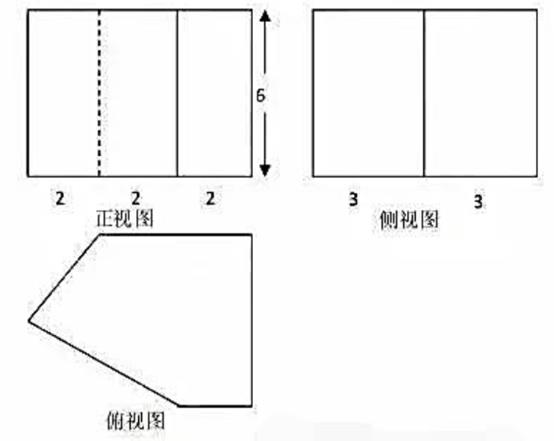 A、158 B、162 C、182 D、322. 已知某几何体的三视图如图所示,则该几何体的体积为( )
A、158 B、162 C、182 D、322. 已知某几何体的三视图如图所示,则该几何体的体积为( ) A、 B、 C、 D、3. 如图,扇形OAB的圆心角为90°,半径为1,则该扇形绕OB所在直线旋转一周得到的几何体的表面积为( )
A、 B、 C、 D、3. 如图,扇形OAB的圆心角为90°,半径为1,则该扇形绕OB所在直线旋转一周得到的几何体的表面积为( ) A、 B、2π C、3π D、4π4. 在四面体 中, 是边长为 的等边三角形, , , ,则四面体 的体积为( )A、 B、 C、 D、5. 如图,正方形 的边长为 2, 分别为 的中点,沿 将正方形折起,使 重合于点 ,构成四面体 ,则四面体 的体积为( )
A、 B、2π C、3π D、4π4. 在四面体 中, 是边长为 的等边三角形, , , ,则四面体 的体积为( )A、 B、 C、 D、5. 如图,正方形 的边长为 2, 分别为 的中点,沿 将正方形折起,使 重合于点 ,构成四面体 ,则四面体 的体积为( ) A、 B、 C、 D、6. 某几何体由一个棱柱与一个棱锥组合而成,其三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )
A、 B、 C、 D、6. 某几何体由一个棱柱与一个棱锥组合而成,其三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )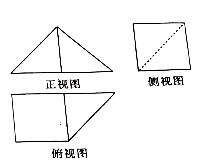 A、 B、 或 C、 D、 或7. 两个圆锥和一个圆柱分别有公共底面,且两圆锥的顶点和底面的圆周都在同一球面上.若圆柱的侧面积等于两个圆锥的侧面积之和,且该球的表面积为 ,则圆柱的体积为( )A、 B、 C、 D、8. 某几何体的三视图如图所示,则该几何体的体积V=( )
A、 B、 或 C、 D、 或7. 两个圆锥和一个圆柱分别有公共底面,且两圆锥的顶点和底面的圆周都在同一球面上.若圆柱的侧面积等于两个圆锥的侧面积之和,且该球的表面积为 ,则圆柱的体积为( )A、 B、 C、 D、8. 某几何体的三视图如图所示,则该几何体的体积V=( ) A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体的体积为( )
A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体的体积为( ) A、 B、 C、 D、10. 如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A、 B、 C、 D、11. 某几何体的三视图如图所示,则该几何体的体积为( )
A、 B、 C、 D、10. 如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A、 B、 C、 D、11. 某几何体的三视图如图所示,则该几何体的体积为( )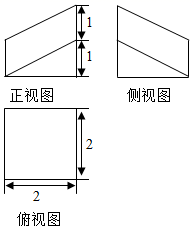 A、2 B、4 C、6 D、812. 已知直三棱柱 的顶点都在球 的球面上, , ,若球 的表面积为 ,则这个直三棱柱的体积是( )A、16 B、15 C、 D、
A、2 B、4 C、6 D、812. 已知直三棱柱 的顶点都在球 的球面上, , ,若球 的表面积为 ,则这个直三棱柱的体积是( )A、16 B、15 C、 D、二、填空题
-
13. 某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为.
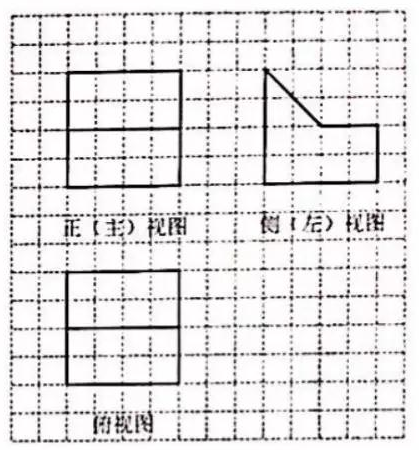 14. 在四面体 中, ,二面角 的大小为 ,则四面体 外接球的半径为 .15. 某几何体的三视图如图所示,则该几何体的体积是;表面积是 .
14. 在四面体 中, ,二面角 的大小为 ,则四面体 外接球的半径为 .15. 某几何体的三视图如图所示,则该几何体的体积是;表面积是 . 16. 已知四棱锥 的底面是边长为 的正方形,且四棱锥 的顶点都在半径为2的球面上,则四棱锥 体积的最大值为.17. 设三棱锥 的三条侧棱两两垂直,且 ,则三棱锥 的体积是 .18. 连接正方体每个面的中心构成一个正八面体,则该八面体的外接球与内切球体积之比为 。
16. 已知四棱锥 的底面是边长为 的正方形,且四棱锥 的顶点都在半径为2的球面上,则四棱锥 体积的最大值为.17. 设三棱锥 的三条侧棱两两垂直,且 ,则三棱锥 的体积是 .18. 连接正方体每个面的中心构成一个正八面体,则该八面体的外接球与内切球体积之比为 。三、解答题

