初中数学浙教版七年级上册5.4 一元一次方程的应用(1) 同步训练
试卷更新日期:2019-10-31 类型:同步测试
一、单选题
-
1. 小张早晨去学校共用时15分,他跑了一段,走了一段,他跑步的平均速度是250米/分,步行的平均速度是80米/分,他家离学校的距离是2900米,设他跑步的时间为x分,根据题意,可列出的方程是( )A、250x+80(15﹣x)=2900 B、80x+250(15﹣x)=2900 C、80x+250x=2900 D、250x+80(15+x)=29002. 中国古代人民很早就在生产生活种发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有x辆车,则可列方程( )A、3(x﹣2)=2x+9 B、3(x+2)=2x﹣9 C、 +2= D、 ﹣2=3. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架. 它的代数成就主要包括开方术、正负术和方程术. 其中,方程术是《九章算术》最高的数学成就. 《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六. 问人数、鸡价各几何?”
译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱; 如果每人出六钱,那么少了十六钱. 问:有几个人共同出钱买鸡?鸡的价钱是多少?”则共同出钱的人数和鸡的价钱分别为( )
A、9人,70钱 B、9人,81钱 C、8人,70钱 D、10人,81钱4. 小明买书需用34元钱,付款时恰好用了1元和5元的纸币共10张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A、x+10(x-50)=34 B、x+5(10-x)=34 C、x+5(x-10)=34 D、5x+(10-x)=345. 下面是两位同学的对话,根据对话内容,可求出这位同学的年龄是( ) A、11岁 B、12岁 C、13岁 D、14岁6. 一个两位数的个位数字与十位数字都是,如果将个位数字与十位数字分别加2和1,所得新数比原数大12,则可列的方程是( )A、2x+3=12 B、10x+2+3=12 C、(10x+x)-10(x+1)-(x+2)=12 D、10(x+1)+(x+2)=10x+x+127. 三个连续奇数的和是81,则中间一个奇数是( )A、23 B、25 C、27 D、298. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和8港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、
A、11岁 B、12岁 C、13岁 D、14岁6. 一个两位数的个位数字与十位数字都是,如果将个位数字与十位数字分别加2和1,所得新数比原数大12,则可列的方程是( )A、2x+3=12 B、10x+2+3=12 C、(10x+x)-10(x+1)-(x+2)=12 D、10(x+1)+(x+2)=10x+x+127. 三个连续奇数的和是81,则中间一个奇数是( )A、23 B、25 C、27 D、298. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和8港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、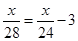 B、
B、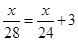 C、
C、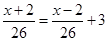 D、
D、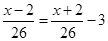 9. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?“其意思为:速度快的人走100步,速度慢的人只走60步,现速度慢的人先走100步,速度快的人去追赶,则速度快的人要走步才能追到速度慢的人.10. A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
9. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?“其意思为:速度快的人走100步,速度慢的人只走60步,现速度慢的人先走100步,速度快的人去追赶,则速度快的人要走步才能追到速度慢的人.10. A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
A、4小时 B、4.5小时 C、5小时 D、4小时或5小时二、填空题
-
11. 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有两.(注:明代时1斤=16两,故有“半斤八两”这个成语)
 12. 把50分成两个数的和,使第一个数加2,与第二个数减4的结果相同,则第一个数是 .13. 三个连续奇数的和是 75,这三个数分别是 .14. 如果某一年的7月份中,有4个星期六,它们的日期之和为70,那么这个月的18日是星期 .15. 父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米 小时,如果再载了另一个人,则速度为20千米 小时 摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为小时.
12. 把50分成两个数的和,使第一个数加2,与第二个数减4的结果相同,则第一个数是 .13. 三个连续奇数的和是 75,这三个数分别是 .14. 如果某一年的7月份中,有4个星期六,它们的日期之和为70,那么这个月的18日是星期 .15. 父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米 小时,如果再载了另一个人,则速度为20千米 小时 摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为小时.三、解答题
-
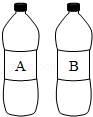
16. 食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A.B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A.B两种饮料共100瓶,问A.B两种饮料各生产了多少瓶?
 17. 大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句话的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚.求笼中各有几只鸡和兔?
17. 大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句话的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚.求笼中各有几只鸡和兔?原来孙子提出了大胆的设想,他假设砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独脚鸡”,而每只免就变成了“双脚免”,这样,“独脚鸡”和“双脚免”的脚就由94只变成了47只;而每只“鸡”的头数与脚数之比变为1:1,每只“兔”的头数与脚数之比变为1:2.由此可知,有一只“双脚兔”,脚的数量就会比头的数量多1.所以,“独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数,即:47﹣35=12(只);鸡的数量就是35﹣12=23(只).当然,这道题还可以用方程来解答,请同学们用方程的思想解答此题.
18. 如图,在数轴上,点A表示-5,点B表示10.动点P从点A出发,沿数轴正方向以每秒1个单位的速度匀速运动;同时,动点Q从点B出发,沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.
(1)、当t为多少秒时,P,Q两点相遇,求出相遇点所对应的数;(2)、当t为何值时,P,Q两点的距离为3个单位长度,并求出此时点P对应的数.