备考2020年高考数学一轮复习:32 二元一次不等式(组)与简单的线性规划问题
试卷更新日期:2019-10-31 类型:一轮复习
一、单选题
-
1. 若实数x,y满足约束条件 ,则z=3x+2y的最大值是( )A、-1 B、1 C、10 D、122. 设变量 满足约束条件 则目标函数 的最大值为( )A、2 B、3 C、5 D、63. 已知 、 是不等式组 所表示的平面区域内的两个不同的点,则 的最大值是( )A、
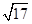 B、
B、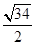 C、
D、
C、
D、 4. 已知平面区域如图所示, 在平面区域内取得最大值的最优解有无数多个,则 的值为( )
4. 已知平面区域如图所示, 在平面区域内取得最大值的最优解有无数多个,则 的值为( ) A、 B、 C、 D、不存在5. 已知实数x,y满足 ,如果目标函数z=x-y的最小值为-1,则实数m等于( )A、7 B、5 C、4 D、36. 已知 , , ,平面区域 是由所有满足 的点 组成的区域,则区域 的面积是( ).A、8 B、12 C、16 D、207. 已知 , 满足约束条件 ,若目标函数 可在点 处取得最大值,则 的取值范围为( )A、 B、 C、 D、8. 已知变量 满足约束条件 ,则 的取值范围是( )A、 B、 C、 D、9. 下列点中,在不等式3x+2y-6>0表示的平面区域内的是( )A、(0,0) B、(1,0) C、(1,1) D、(1,2)10. 若实数x,y满足约束条件: ,则z=x+y的最大值是( )A、3 B、1 C、-2 D、211. 设 , 满足约束条件 ,则目标函数 取最小值时的最优解 是( )A、 B、 C、 D、12. 某服装缝纫店现有7m²的羊毛料,9m²的棉布料,做一条裙子需要羊毛料1m²的和1m²的棉布料,做一条裤子需要1m²的羊毛料和2m²的棉布料,一条裙子的纯收益是30元,一条裤子的纯收益是40元,服装制造商获得的最大收益是( )A、150元 B、180元 C、210元 D、230元
A、 B、 C、 D、不存在5. 已知实数x,y满足 ,如果目标函数z=x-y的最小值为-1,则实数m等于( )A、7 B、5 C、4 D、36. 已知 , , ,平面区域 是由所有满足 的点 组成的区域,则区域 的面积是( ).A、8 B、12 C、16 D、207. 已知 , 满足约束条件 ,若目标函数 可在点 处取得最大值,则 的取值范围为( )A、 B、 C、 D、8. 已知变量 满足约束条件 ,则 的取值范围是( )A、 B、 C、 D、9. 下列点中,在不等式3x+2y-6>0表示的平面区域内的是( )A、(0,0) B、(1,0) C、(1,1) D、(1,2)10. 若实数x,y满足约束条件: ,则z=x+y的最大值是( )A、3 B、1 C、-2 D、211. 设 , 满足约束条件 ,则目标函数 取最小值时的最优解 是( )A、 B、 C、 D、12. 某服装缝纫店现有7m²的羊毛料,9m²的棉布料,做一条裙子需要羊毛料1m²的和1m²的棉布料,做一条裤子需要1m²的羊毛料和2m²的棉布料,一条裙子的纯收益是30元,一条裤子的纯收益是40元,服装制造商获得的最大收益是( )A、150元 B、180元 C、210元 D、230元二、填空题
-
13. 若x,y满足 .则y-x的最小值为 , 最大值为.14. 若变量 满足约束条件 ,则目标函数 的最大值为.15. 若实数x,y满足约束条件 ,则z= x-y最小值是 , x2+y2的最小值是 .16. 若 满足约束条件 ,则 的最小值为 .17. 已知A(1,2),B(-2,1),O为坐标原点.若直线l:ax+by=2与△ABO所围成区域(包含边界)没有公共点,则a-b的取值范围为 .18. 某农户计划种植莴笋和西红柿,种植面积不超过 亩,投入资金不超过 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩
年种植成本/亩
每吨售价
莴笋
5吨
1万元
0.5万元
西红柿
4.5吨
0.5万元
0.4万元
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为万元
三、解答题
-
19. 已知实数x,y满足 ,求z=2x+y的最大值和最小值.20. 若 , 满足约束条件 .(1)、求目标函数 的最值;(2)、求目标函数 的最值.21. 某家俱公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数据如下:
工艺要求
产品甲
产品乙
生产能力/(台/天)
制白坯时间/天
6
12
120
油漆时间/天
8
4
64
单位利润/元
200
240
问该公司如何安排甲、乙二种柜的日产量可获最大利润,并且最大利润是多少?
22. 电视台应某企业之约播放两套连续剧,其中,连续剧甲每次播放时间80分钟,其中广告时间1分钟,收视观众60万;连续剧乙每次播放时间40分钟,其中广告时间1分钟,收视观众20万.现在企业要求每周至少播放广告6分钟,而电视台每周至多提供320分钟节目时间.(1)、设每周安排连续剧甲 次,连续剧乙 次,列出 , 所应该满足的条件;(2)、应该每周安排两套电视剧各多少次,收视观众最多?