初中数学北师大版七年级上学期第三章 3.5 探索与表达规律

试卷更新日期：2019-10-30 类型：同步测试

进入出卷网下载

一、单选题

1. ……依次观察左边三个图形，并判断照此规律从左到右第2019个图形是（）

A、 B、 C、 D、

查看试题解析
2. 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和，下列等式中，符合这一规律的表达式为（）

A、 $13 = 3 + 10$ B、 $25 = 9 + 16$ C、 $49 = 18 + 31$ D、 $64 = 28 + 36$

查看试题解析
3. 利用如图1的二维码可以进行身份识别.某校建市了一个身份识别系统，图2是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×2³+b×2²+c×2¹+d×2⁰ ，如图2第一行数字从左到右依次为0，1，0，1，序号为0×2³+1×2²+0×2¹+1×2⁰=5，表示该生为5班学生.下图表示6班学生的识别图案是（）

A、 B、 C、 D、

查看试题解析
4. 将正整数按如图所示的规律排列下去，若有序数对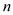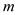（，）表示第n排，从左到右第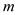个数，如（4，2）表示9，则表示114的有序数对是（）

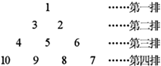A、（15，9） B、（9，15） C、（15，7） D、（7，15）

查看试题解析
5. 计算 $\frac{1}{1 \times 3}$ + $\frac{1}{3 \times 5}$ + $\frac{1}{5 \times 7}$ + $\frac{1}{7 \times 9}$ +…+ $\frac{1}{37 \times 39}$ 的结果是（）

A、 $\frac{19}{37}$ B、 $\frac{19}{39}$ C、 $\frac{37}{39}$ D、 $\frac{38}{39}$

查看试题解析
6. 如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a₁ ，第2幅图形中“●”的个数为a₂ ，第3幅图形中“的个数为a₃ ， …，以此类推，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + ... \frac{1}{a_{18}}$ 的值为（）

A、 $\frac{19}{20}$ B、 $\frac{19}{40}$ C、 $\frac{531}{760}$ D、 $\frac{589}{840}$

查看试题解析
7. 下面摆放的图案，从第二个起，每个都是前一个按顺时针方向旋转90°得到，第2019个图案中箭头的指向是（）

A、上方 B、右方 C、下方 D、左方

查看试题解析

二、填空题

8. 定义： $a$ 为不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为 $a$ 的差倒数.如：2的差倒数是 $\frac{1}{1 - 2} = - 1$ ，－1的差倒数是 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ .已知 $a_{1} = - \frac{1}{2}$ ， $a_{2}$ 是 $a_{1}$ 的差倒数， $a_{3}$ 是 $a_{2}$ 的差倒数， $a_{4}$ 是 $a_{3}$ 的差倒数，…，以此类推，则 $a_{2019} =$ .

查看试题解析
9. 古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律性，则第1007个三角数与第1009个三角数的差为.

查看试题解析
10. 观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2019个图形中共有个〇.

查看试题解析

初中数学北师大版七年级上学期 第三章 3.5 探索与表达规律

一、单选题

二、填空题

初中数学北师大版七年级上学期第三章 3.5 探索与表达规律