2017年山东省泰安市高考数学二模试卷（理科）

试卷更新日期：2017-07-11 类型：高考模拟

进入出卷网下载

一、选择题

1. 复数z满足（z﹣i）（2﹣i）=5．则z=（）

A、﹣2﹣2i B、﹣2+2i C、2﹣2i D、2+2i

查看试题解析
2. 设全集U=R，集合A={x|x＞1}，集合B={x|x＞p}，若（∁_UA）∩B=∅，则p应该满足的条件是（）

A、p＞1 B、p≥1 C、p＜1 D、p≤1

查看试题解析
3. 已知命题p：“m=﹣1”，命题q：“直线x﹣y=0与直线x+m²y=0互相垂直”，则命题p是命题q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要

查看试题解析
4. 已知l是直线，α、β是两个不同平面，下列命题中的真命题是（）

A、若l∥α，l∥β，则α∥β B、若α⊥β，l∥α，则l⊥β C、若l⊥α，l∥β，则α⊥β D、若l∥α，α∥β，则l∥β

查看试题解析
5. 秦九昭是我国南宋时期的数学家，他在所著的《数学九章》中提出的多项式求值的秦九昭算法，至今仍是比较先进的算法，如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例，若输入n，x的值分别为3，4，则输出y的值为（）

A、6 B、25 C、100 D、400

查看试题解析
6. 已知cos（x﹣ $\frac{π}{3}$ ）= $\frac{1}{3}$ ，则cos（2x﹣ $\frac{5 π}{3}$ ）+sin²（ $\frac{π}{3}$ ﹣x）的值为（）

A、﹣ $\frac{1}{9}$ B、 $\frac{1}{9}$ C、 $\frac{5}{3}$ D、﹣ $\frac{5}{3}$

查看试题解析
7. 下列选项中，说法正确的是（）

A、若a＞b＞0，则 $l o g_{\frac{1}{2}} a > l o g_{\frac{1}{2}} b$ B、向量 $\vec{a} = (1 ， m) ， \vec{b} = (m ， 2 m - 1)$ （m∈R）共线的充要条件是m=0 C、命题“∀n∈N^* ， 3ⁿ＞（n+2）•2ⁿ^﹣¹”的否定是“∀n∈N^* ， 3ⁿ≥（n+2）•2ⁿ^﹣¹” D、已知函数f（x）在区间[a，b]上的图象是连续不断的，则命题“若f（a）•f（b）＜0，则f（x）在区间（a，b）内至少有一个零点”的逆命题为假命题

查看试题解析
8. 函数 $f (x) = \frac{2^{x} + 1}{2^{x} - 1} \cdot c o s x$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 已知实数x，y满足 ${\begin{matrix} x \geq 0 \\ y \geq 0 \\ \frac{x}{3} + \frac{y}{4} \leq 1 \end{matrix}$ ，则 $\frac{x + 2 y + 3}{x + 1}$ 的取值范围是（）

A、 $[\frac{2}{3} ， 11]$ B、[3，11] C、 $[\frac{3}{2} ， 11]$ D、[1，11]

查看试题解析
10. 已知双曲线Γ： $\frac{y^{2}}{a^{2}}$ ﹣ $\frac{x^{2}}{b^{2}}$ =1（a＞0，b＞0）的上焦点F（0，c）（c＞0），M是双曲线下支上的一点，线段MF与圆x²+y²﹣ $\frac{2 c}{3}$ y+ $\frac{a^{2}}{9}$ =0相切于点D，且|MF|=3|DF|，则双曲线Γ的渐近线方程为（）

A、4x±y=0 B、x±4y=0 C、2x±y=0 D、x±2y=0

查看试题解析

二、填空题

11. 观察下列式子： $\sqrt{1 \times 2} < 2$ ， $\sqrt{1 \times 2} + \sqrt{2 \times 3} < \frac{9}{2} \sqrt{1 \times 2} + \sqrt{2 \times 3} + \sqrt{3 \times 4} < 8$ ， $\sqrt{1 \times 2} + \sqrt{2 \times 3} + \sqrt{3 \times 4} + \sqrt{4 \times 5} < \frac{25}{2}$ ，
…，根据以上规律，第n个不等式是．

查看试题解析
12. △ABC中，三内角A，B，C的对边分别为a、b、c，且 $\frac{c - b}{\sqrt{2} c - a} = \frac{s i n A}{s i n B + s i n C}$ ，则角B= ．

查看试题解析
13. 某几何体的三视图如图所示，该几何体的体积为．

查看试题解析
14. 如图，在边长为2的正方形ABCD中，M是AB的中点，则过C，M，D三点的抛物线与CD围成阴影部分，在正方形ABCD中任取一点P，则点P恰好取自阴影部分的概率为．

查看试题解析
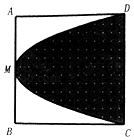15. 已知函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=e^x（x+1），给出下列命题：
①当x＞0时，f（x）=e^﹣^x（x﹣1）；
②函数f（x）有两个零点；
③f（x）＜0的解集为（﹣∞，﹣1）∪（0，1）；
④∀x₁ ， x₂∈R，都有|f（x₁）﹣f（x₂）|＜2．
其中正确的命题为（把所有正确命题的序号都填上）．

查看试题解析

三、解答题

16. 已知函数 $f (x) = s i n (\frac{π}{2} - x) s i n x - \sqrt{3} c o s^{2} x + \frac{\sqrt{3}}{2}$

(1)、求f（x）的最大值及取得最大值时x值；

(2)、若方程 $f (x) = \frac{2}{3}$ 在（0，π）上的解为x₁ ， x₂ ，求cos（x₁﹣x₂）的值．

查看试题解析
17. 已知数列{a_n}的首项为1，S_n为数列{a_n}的前n项和，且满足S_n₊₁=qS_n+1，其中q＞0，n∈N^* ，又2a₂ ， a₃ ， a₂+2成等差数列．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）记b_n=2a_n﹣λ（log₂a_n₊₁）² ，若数列{b_n}为递增数列，求λ的取值范围．

查看试题解析
18. 某公司有A、B、C、D四辆汽车，其中A车的车牌尾号为8，B、C两辆车的车牌尾号为2，D车的车牌尾号为3，已知在非限行日，每辆车都有可能出车或不出车．已知A、D两辆汽车每天出车的概率为 $\frac{2}{3}$ ，B、C两辆汽车每天出车的概率为 $\frac{1}{2}$ ，且四辆汽车是否出车是相互独立的．
该公司所在地区汽车限行规定如下：
车牌尾号
0和5
1和6
2和7
3和8
4和9
限行日
星期一
星期二
星期三
星期四
星期五
（Ⅰ）求该公司在星期二至少有2辆汽车出车的概率；
（Ⅱ）设ξ表示该公司在星期三和星期四两天出车的车辆数之和，求ξ的分布列和数学期望．

查看试题解析
19. 如图所示，直角梯形ABCD两条对角线AC，BD的交点为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，M为线段AB上一点，AM=2MB，且AB⊥BC，AB∥CD，AB=BE=6，CD=BC=3．
（Ⅰ）求证：EM∥平面ADF；
（Ⅱ）求二面角O﹣EF﹣C的余弦值．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{2}}{2}$ ，短轴长为2．直线l：y=kx+m与椭圆C交于M、N两点，又l与直线y= $\frac{1}{2} x 、 y = - \frac{1}{2}$ x分别交于A、B两点，其中点A在第一象限，点B在第二象限，且△OAB的面积为2（O为坐标原点）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求 $\vec{O M} \cdot \vec{O N}$ 的取值范围．

查看试题解析
21. 已知函数f（x）= $\frac{1}{2}$ x²+mx+mlnx
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）当m=1时，若方程f（x）= $\frac{1}{2}$ x²+ac在区间[ $\frac{1}{e}$ ，+∞）上有唯一的实数解，求实数a的取值范围；
（Ⅲ）当m＞0时，若对于区间[1，2]上的任意两个实数x₁ ， x₂ ，且x₁＜x₂ ，都有|f（x₁）﹣f（x₂）|＜x₂²﹣x₁²成立，求实数m的最大值．

查看试题解析

车牌尾号	0和5	1和6	2和7	3和8	4和9
限行日	星期一	星期二	星期三	星期四	星期五