2016-2017学年山东省济宁市曲阜市八年级下学期期中数学试卷

试卷更新日期：2017-07-10 类型：期中考试

进入出卷网下载

一、选择题

1. $\sqrt{1 - x}$ 实数范围内有意义，则x的取值范围是（）

A、x＞1 B、x≥1 C、x＜1 D、x≤1

查看试题解析
2. 下列各组数是三角形的三边，不能组成直角三角形的一组数是（）

A、1，1， $\sqrt{2}$ B、3，4，5 C、5，12，13 D、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$

查看试题解析
3. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
4. 如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（）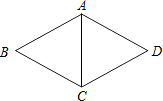

A、5 B、10 C、15 D、20

查看试题解析
5. 已知x、y是实数， $\sqrt{3 x - y}$ +y²﹣6y+9=0，则y^2x的值是（）

A、 $\frac{1}{3}$ B、9 C、6 D、 $\frac{1}{6}$

查看试题解析
6. 下列命题中，真命题是（）

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
7. 下列计算正确的是（）

A、2 $\sqrt{3}$ ×3 $\sqrt{3}$ =6 $\sqrt{3}$ B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、5 $\sqrt{5}$ ﹣2 $\sqrt{2}$ =3 $\sqrt{3}$ D、 $\sqrt{2}$ ÷ $\sqrt{3}$ = $\frac{\sqrt{6}}{3}$

查看试题解析
8. 如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D．则BD的长为（）

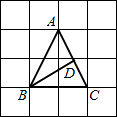A、 $\frac{2}{3} \sqrt{5}$ B、 $\frac{3}{4} \sqrt{5}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{3}{5} \sqrt{5}$

查看试题解析
9. 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=2，则矩形的对角线AC的长是（）

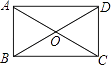A、2 B、4 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
10. 如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 化简 $\sqrt{\frac{5 a^{3}}{6}}$ 的结果是．

查看试题解析
12. 如图，平行四边形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件使其成为菱形（只填一个即可）．

查看试题解析
13. 如图，在平行四边形ABCD中，∠A=45°，BC= $\sqrt{2}$ cm，则AB与CD之间的距离为cm．

查看试题解析
14. 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=度．

查看试题解析
15.
如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为．

查看试题解析

三、解答题

16. 计算：

(1)、（ $\sqrt{24}$ ﹣ $\sqrt{\frac{1}{2}}$ ）﹣（ $\sqrt{\frac{1}{8}}$ + $\sqrt{6}$ ）；

(2)、（ $\sqrt{2}$ +1）（ $\sqrt{2}$ ﹣1）

查看试题解析
17. 在如图所示的4×4方格中，每个小方格的边长都为1

(1)、
在图（1）中画出长度为 $\sqrt{17}$ 的线段，要求线段的端点在格点上；

(2)、
在图（2）中画出一个三条边长分别为3，2 $\sqrt{2}$ ， $\sqrt{5}$ 的三角形，使它的端点都在格点上．

查看试题解析
18. 已知：如图，在▱ABCD中，对角线AC，BD相交于点O．∠1=∠2．求证：▱ABCD是矩形．

查看试题解析
19. 某中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m．

(1)、试判断△BCD的形状；

(2)、若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
20. 如图，已知四边形ABDE是平行四边形，C为边BD延长线上一点，连结AC、CE，使AB=AC．

(1)、求证：△BAD≌△ACE；

(2)、若∠B=30°，AB=26，BD=10，求平行四边形ABDE的面积．

查看试题解析
21. 阅读下面的文字，解答问题．
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，但是由于1＜ $\sqrt{2}$ ＜2，所以 $\sqrt{2}$ 的整数部分为1，将 $\sqrt{2}$ 减去其整数部分1，差就是小数部分 $\sqrt{2}$ ﹣1，根据以上的内容，解答下面的问题：

(1)、 $\sqrt{5}$ 的整数部分是，小数部分是；

(2)、1+ $\sqrt{2}$ 的整数部分是，小数部分是；

(3)、若设2+ $\sqrt{3}$ 整数部分是x，小数部分是y，求x﹣ $\sqrt{3}$ y的值．

查看试题解析
22. 我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．

(1)、
如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．
求证：中点四边形EFGH是平行四边形；

(2)、
如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；

(3)、若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）

查看试题解析