2016-2017学年湖北省鄂州市梁子湖区九年级下学期期中数学试卷

试卷更新日期：2017-07-10 类型：期中考试

进入出卷网下载

一、选择题

1. 下列四个数中，正整数是（）

A、﹣2 B、﹣1 C、0 D、1

查看试题解析
2. 下列等式一定成立的是（）

A、2a+3b=5ab B、（a³）²=a⁵ C、a²•a³=a⁵ D、（a+b）²=a²+b²

查看试题解析
3. 地球与月球之间的平均距离是38.4万千米，数据“38.4万”用科学记数法表示为（）

A、38.4×10⁴ B、3.84×10⁵ C、3.84×10⁶ D、3.84×10⁴

查看试题解析
4. 如图所示的几何体为圆台，其俯视图正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列说法正确的是（）

A、若一组数据x₁ ， x₂ ， x₃的方差为1，则另一组数据2x₁ ， 2x₂ ， 2x₃的方差为4 B、调查某批次汽车的抗撞击能力，应选择全面调查 C、中位数就是一组数据中最中间的一个数 D、8，9，9，10，10，11这组数据的众数是10

查看试题解析
6. 如图，直线a∥b，三角尺的直角顶点在直线b上，若∠1=50°，则∠2等于（）

A、50° B、40° C、45° D、25°

查看试题解析
7.
如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△ABC的边上一动点，沿B→A→C的路径移动，过点P作PD⊥BC于点D，设BD=x，△BDP的面积为y，则y与x函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧 $\hat{B C}$ 于点D，连接CD、OD．下列结论：①AC∥OD；②CE=OE；③∠OED=∠AOD；④CD=DE．其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，抛物线y=ax²+bx+c（a≠0）与y轴的正半轴相交，顶点在第四象限，对称轴为x=1，下列结论：①b＜0；②a+b＜0；③ $\frac{b}{c}$ ＜﹣2；④an²+bn=a（2﹣n）²+b（2﹣n）（n为任意实数），其中正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10.
如图，在Rt△ABC中，∠ACB=90°，AC=2 $\sqrt{3}$ ，BC=6，动点P，Q分别在边AB，BC上，则CP+PQ的最小值为（）

A、3 $\sqrt{3}$ B、3+ $\frac{3 \sqrt{3}}{2}$ C、2 $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析

二、填空题

11. 的算术平方根是 $\sqrt{2}$ ．

查看试题解析
12. 分解因式：x³﹣9x= ．

查看试题解析
13. 用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径为．

查看试题解析
14. 如图，已知点A是双曲线y= $\frac{2}{x}$ 在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= $\frac{k}{x}$ （k＜0）上运动，则k的值是．

查看试题解析
15. 在平面直角坐标系中，已知A（﹣3，0），B（0，4），C（1，m），当△ABC是直角三角形时，m的值为．

查看试题解析
16.
如图，正方形ABCD的四个顶点在坐标轴上，点A的坐标为（﹣3，0），假设有甲，乙两个物体分别由点A同时出发，沿正方形ABCD的边作环绕运动，物体甲按顺时针方向匀速运动，物体乙按逆时针方向匀速运动，若物体甲12秒钟可环绕一周回到点A，物体乙24秒钟可环绕一周回到点A，则两个物体运动后的第2017次相遇地点的坐标是．

查看试题解析

三、解答题

17. 先化简，再求值：（ $\frac{x}{x + y}$ + $\frac{2 y}{x + y}$ ）• $\frac{x y}{x + 2 y}$ ÷（ $\frac{1}{x}$ + $\frac{1}{y}$ ），其中x²+y²=17，（x﹣y）²=9．

查看试题解析
18. 如图，△ABC中，BD、CE分别是AC、AB上的中线，BD与CE相交于点O，点M、N分别是OB、OC的中点，连接DE、EM、MN、ND．

(1)、求证：四边形DEMN是平行四边形；

(2)、若四边形DEMN是菱形，且BC=4cm，AC=6cm，求边AB的长．

查看试题解析
19. 为了解市民对全市创卫工作的满意程度，某中学数学兴趣小组在全市甲，乙两个区内进行了调查统计，将调查结果分为很满意，满意，不满意，很不满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．
请结合图中信息，解决下列问题：

(1)、参加这次调查的总人数为人，其中调查结果为“满意”的人数是人，调查结果为“很不满意”的人数占总人数的百分比为，扇形图中“不满意”部分对应扇形的圆心角为度．

(2)、兴趣小组准备从调查结果为“很不满意”的4位市民中随机选择2位进行回访，已知这4位市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自甲区的概率．

查看试题解析
20. 关于x的方程x²+（2k+1）x+k²+2=0有两个实数根x₁、x₂

(1)、求实数k的取值范围；

(2)、若x₁、x₂满足|x₁|+|x₂|=|x₁x₂|﹣1，求k的值．

查看试题解析
21.
如图所示，港口B位于港口O正西方向120km处，小岛C位于港口O北偏西60°的方向．一艘游船从港口O出发，沿OA方向（北偏西30°）以vkm/h的速度驶离港口O，同时一艘快艇从港口B出发，沿北偏东30°的方向以60km/h的速度驶向小岛C，在小岛C用1h加装补给物资后，立即按原来的速度给游船送去．

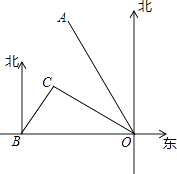(1)、快艇从港口B到小岛C需要多长时间？

(2)、若快艇从小岛C到与游船相遇恰好用时1h，求v的值及相遇处与港口O的距离．

查看试题解析
22. 如图，⊙O是等边△ABC的外接圆，M是BC延长线上一点，连接AM交⊙O于点D，延长BD至点N，使得BN=AM，连接CN，MN．

(1)、判断△CMN的形状，并证明你的结论；

(2)、求证：CN是⊙O的切线；

(3)、若等边△ABC的边长是2，求AD•AM的值．

查看试题解析
23. 某公司生产的商品市场指导价为每千克150元，公司的实际销售价格可以浮动x个百分点（即销售价格=150（1+x%）），经过市场调研发现，这种商品的日销售量p（千克）与销售价格浮动的百分点x之间的函数关系为p=﹣2x+24．若该公司按浮动﹣12个百分点的价格出售，每件商品仍可获利10%．

(1)、求该公司生产销售每千克商品的成本为多少元？

(2)、当该公司的商品定价为多少元时，日销售利润为576元？（说明：日销售利润=（销售价格一成本）×日销售量）

(3)、该公司决定每销售一千克商品就捐赠a元利润（a≥1）给希望工程，公司通过销售记录发现，当价格浮动的百分点大于﹣1时，扣除捐赠后的日销售利润随x的增大而减小，直接写出a的取值范围．

查看试题解析
24. 已知抛物线C₁：y=x²+2x﹣3与x轴交于点A，B（点A在点B左侧），与y轴交于点C，抛物线C₂：y=ax²+bx+c经过点B，与x轴的另一个交点为E（﹣4，0），与y轴交于点D（0，2）．

(1)、求抛物线C₂的解析式；

(2)、
设点P为线段AB上一动点（点P不与点A，B重合），过点P作x轴的垂线交抛物线C₁于点M，交抛物线C₂于点N．
①当四边形AMBN的面积最大时，求点P的坐标；
②当CM=DN≠0时，求点P的坐标．

查看试题解析