初中数学浙教版九年级上册4.6 相似多边形 强化提升训练
试卷更新日期：2019-10-26 类型：同步测试
一、单选题
-
1. 如图，在矩形ABCD中，E，F分别为，AD与BC的中点，且矩形ABCD∽矩形AEFB， 的值为（ ）
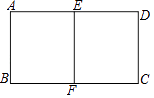A、2 B、 C、 D、2. 若两个相似矩形的相似比为 ，较小矩形面积为 ，较大矩形一边为 ，则其相邻的一边是（ ）A、 B、 C、 D、3. 如图，E、F分别在矩形ABCD的边CD、AB上，EF⊥AB，G、H分别是BC、EF的中点，EH＞HG，除矩形EFBC外，图中4个矩形都彼此相似，若BC=1，则AB等于（ ）
A、 B、 C、 D、二、填空题
-
4. 两个相似多边形的一组对应边分别为3cm和4.5cm，如果它们的面积之和为130cm2 ， 那么较小的多边形的面积是cm2 ．
5. 如图，四边形ABCD和A1B1C1D1相似，已知 ，AB=10，A1B1=16，CD=18，则 =°，C1D1= ， 它们的相似比为 ．
6. 如图，正方形 的边长是 ，除 和 四点外，图形的其他顶点均为所在的一条线段的中点，则从正方形 中挖掉阴影部分后，所剩下部分面积等于 ．
7. 如图，在矩形ABCD中，E是AD上一点，把△ABE沿直线BE翻折，点A正好落在BC边上的点F处，如果四边形CDEF和矩形ABCD相似，那么四边形CDEF和矩形ABCD面积比是 ．
三、解答题
-
8. 已知四边形ABCD与四边形A1B1C1D1相似，且A1B1：B1C1：C1D1：D1A1=7：8：11：14，若四边形ABCD的周长为40，求四边形ABCD各边的长．
9. 若四边形ABCD与四边形A1B1C1D1相似，相似比为k1= ，又四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为k2= ，请问四边形ABCD与四边形A2B2C2D2相似吗？若相似，相似比是多少？
10. 根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．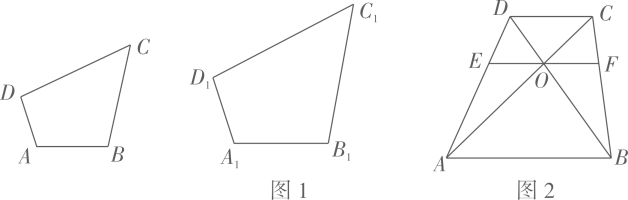
(1)、某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．①条边成比例的两个凸四边形相似；（命题）
②三个角分别相等的两个凸四边形相似；（命题）
③两个大小不同的正方形相似．（命题）
(2)、如图1，在四边形ABCD和四边形A1B1C1D1中，∠ABC＝∠A1B1C1 ， ∠BCD＝∠B1C1D1 ， ，求证：四边形ABCD与四边形A1B1C1D1相似．(3)、如图2，四边形ABCD中，AB∥CD ， AC与BD相交于点O ， 过点O作EF∥AB分别交AD ， BC于点E ， F ． 记四边形ABFE的面积为S1 ， 四边形EFDE的面积为S2 ， 若四边形ABFE与四边形EFCD相似，求 的值．11. 阅读下列材料，完成任务：自相似图形
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．
任务：
(1)、图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；(2)、如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为；(3)、现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答．
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含b的式子表示）；
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）．