初中数学浙教版九年级上册4.5 相似三角形的性质及应用(3) 同步训练
试卷更新日期:2019-10-25 类型:同步测试
一、基础夯实
-
1. 小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶( )A、0.5m B、0.55m C、0.6m D、2.2m2. 如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
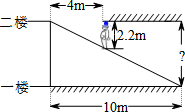 A、 B、 C、11m D、3. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.
A、 B、 C、11m D、3. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.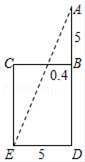 4. 小明家的客厅有一张直径BC为1.2米,高0.8米的圆桌,在距地面2米的A处有一盏灯,BC的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是 。
4. 小明家的客厅有一张直径BC为1.2米,高0.8米的圆桌,在距地面2米的A处有一盏灯,BC的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是 。 5. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
5. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )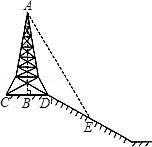 A、24m B、22m C、20m D、18m6. 如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.
A、24m B、22m C、20m D、18m6. 如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.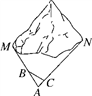 7. 如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE , 已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=m.
7. 如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE , 已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=m. 8. 如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
8. 如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
A、3倍 B、不知AB的长度,无法计算 C、 D、9. 如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则击球的高度h为. 10. 我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。
10. 我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。
二、强化提升
-
11. 为了测量一棵大树的高度,准备了如下测量工具:①镜子;②皮尺;③长为2m的标杆;④高为1.5m的测角仪(能测量仰角和俯角的仪器),请根据你所设计的测量方案,回答下列问题:
 (1)、在你设计的方案上,选用的测量工具是;(2)、在下图中画出你的测量方案示意图;(3)、你需要测量示意图中的哪些数据,并用a,b,c,α等字母表示测得的数据;(4)、写出求树高的算式:AB= m.12. 一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2 , 请通过计算比较S1与S2的大小.
(1)、在你设计的方案上,选用的测量工具是;(2)、在下图中画出你的测量方案示意图;(3)、你需要测量示意图中的哪些数据,并用a,b,c,α等字母表示测得的数据;(4)、写出求树高的算式:AB= m.12. 一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2 , 请通过计算比较S1与S2的大小.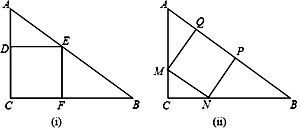 13. 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,身高为1.6m,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
13. 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,身高为1.6m,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.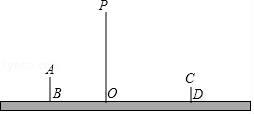 (1)、在小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中分别画出小亮站在B处、D处的影子;(2)、当小亮离开灯杆的距离OB=3.6m时,小亮的影长为1.2m,灯杆的高度为多少m?(3)、当小亮离开灯杆的距离OD=6m时,小亮的影长变为多少m?14. 如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
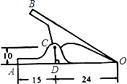
(1)、在小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中分别画出小亮站在B处、D处的影子;(2)、当小亮离开灯杆的距离OB=3.6m时,小亮的影长为1.2m,灯杆的高度为多少m?(3)、当小亮离开灯杆的距离OD=6m时,小亮的影长变为多少m?14. 如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似? 15. 如图是一个常见铁夹的侧面示意图, , 表示铁夹的两个面, 是轴, 于点 ,已知 , , ,我们知道铁夹的侧面是轴对称图形,请求出 、 两点间的距离.
15. 如图是一个常见铁夹的侧面示意图, , 表示铁夹的两个面, 是轴, 于点 ,已知 , , ,我们知道铁夹的侧面是轴对称图形,请求出 、 两点间的距离.