初中数学浙教版九年级上册4.5 相似三角形的性质及应用（1） 同步训练

试卷更新日期：2019-10-25 类型：同步测试

进入 出卷网 下载

一、基础夯实

  • 1. 三角形的重心是三条（   ）
    A、中线的交点 B、角平分线的交点 C、高线的交点 D、垂线的交点

    查看试题解析

  • 2. 如图，已知点D是△ABC的重心，若AE＝4，则AC的长度为（    ）

    A、4 B、8 C、10 D、12

    查看试题解析

  • 3. 过△ABC的重心G作GE∥BC交AC于点E，线段BC=12，线段GE长为（ ）
    A、4 B、4.5 C、6 D、8

    查看试题解析

  • 4. 如图，若点G是△ABC的重心，GD∥BC，则 GDBC = ．

    查看试题解析

  • 5. 已知点G是△ABC的重心，AG=8，那么点G与边BC中点之间的距离是 ．

    查看试题解析

  • 6. 已知 △ABC 是等边三角形，边长为3，G是三角形的重心，那么GA的长度为 ．

    查看试题解析

  • 7. 如图所示，已知点G为Rt△ABC的重心，∠ABC=90°，若AB=12cm，BC=9cm，则△AGD的面积是 ．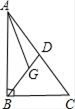

    查看试题解析

  • 8. 如图，已知点G为△ABc的重心，过点G作DE∥BC。交AB于点D，交AC于点E，若BC=15，则线段DE的长为 ．

    查看试题解析

  • 9. 如图，点G是△ABC的重心，GH⊥BC，垂足为点H，若GH=3，则点A到BC的距离为 ．

    查看试题解析

二、强化提升

  • 10. 如图，△ABC中，G为重心，DF∥BC，则 FGAE =.

    查看试题解析

  • 11. 如图，△ABC中，∠BAC=90°，点G是△ABC的重心，如果AG=4，那么BC的长为    

    查看试题解析

  • 12. 如图，G为△ABC的重心，若EF过点G，且EF∥BC，交AB，AC于E，F，则 EFBC ＝ ．

    查看试题解析

  • 13. 如图，△ABC中，∠BAC=90°，点G是△ABC的重心，如果AG=4，那么BC=.

    查看试题解析

  • 14. 已知AM是△ABC中BC边上的中线，P是△ABC的重心，过P作EF（EF∥BC），分别交AB、AC于E、F，则 BEAE+CFAF = ．

    查看试题解析

  • 15. 如图所示，设M是△ABC的重心，过M的直线分别交边AB，AC于P，Q两点，且 APPB =m， AQQC =n ，则 1m + 1n = ．

    查看试题解析

  • 16. 在△ ABC 中，已知 D 是 BC 边的中点， G 是△ ABC 的重心，过 G 点的直线分别交 AB 、 AC 于点 E 、 F .

    (1)、如图1，当 EF ∥ BC 时，求证： BEAE+CFAF=1 ；
    (2)、如图2，当 EF 和 BC 不平行，且点 E 、 F 分别在线段 AB 、 AC 上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.
    (3)、如图3，当点 E 在 AB 的延长线上或点 F 在 AC 的延长线上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.

    查看试题解析