初中数学浙教版九年级上册4.4 两个三角形相似的判定(2) 同步训练
试卷更新日期:2019-10-25 类型:同步测试
一、单选题
-
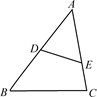
1. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且∠AED=∠B,再将下列四个选项中的一个作为条件,不一定能使得△ADE和△BDF相似的是( )
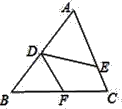 A、 B、 C、 D、2. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
A、 B、 C、 D、2. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、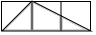 B、
B、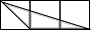 C、
C、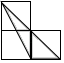 D、
D、 3. 如图,下列条件不能判定△ADB~△ABC的是( )
3. 如图,下列条件不能判定△ADB~△ABC的是( )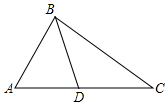 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD·AC D、
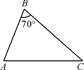
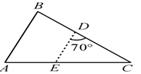
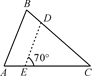
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD·AC D、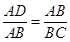 4. 如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形相似的有( ).
4. 如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形相似的有( ).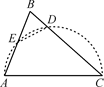
 A、1个 B、2个 C、3个 D、4个5. 如图,已知∠1=∠2,若再增加一个条件不一定能使结论△ADE∽△ABC成立,则这个条件是( )
A、1个 B、2个 C、3个 D、4个5. 如图,已知∠1=∠2,若再增加一个条件不一定能使结论△ADE∽△ABC成立,则这个条件是( ) A、
A、 B、
B、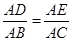 C、
C、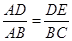 D、
D、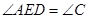 6. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC如图1相似的三角形所在网格图形是( )
6. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC如图1相似的三角形所在网格图形是( )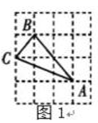 A、
A、 B、
B、 C、
C、 D、
D、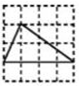 7. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、
7. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、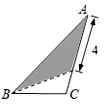 B、
B、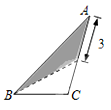 C、
C、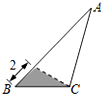 D、
D、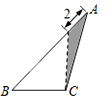 8. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
8. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) A、(6,5) B、(6,0) C、(6,4) D、(4,2)
A、(6,5) B、(6,0) C、(6,4) D、(4,2)二、填空题
-
9. 如图,DE与BC不平行,当 =时,△ABC与△AED相似.
 10. 如图标记了△ABC与△DEF边、角的一些数据,如果再添加一个条件使△ABC∽△DEF,那么这个条件可以是 . (只填一个即可)
10. 如图标记了△ABC与△DEF边、角的一些数据,如果再添加一个条件使△ABC∽△DEF,那么这个条件可以是 . (只填一个即可)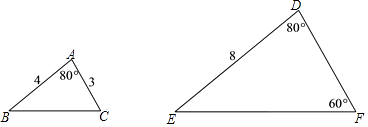 11. 如图,在 中,AC是BC、DC的比例中项,则 ∽ .
11. 如图,在 中,AC是BC、DC的比例中项,则 ∽ .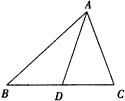 12. 如图, ,BD=4,BC=5,则AC=时,△ACD∽△BDC.
12. 如图, ,BD=4,BC=5,则AC=时,△ACD∽△BDC.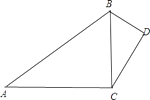
三、解答题
-
13. 已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.
求证:△ACP∽△PDB.
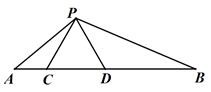 14. 如图,△ABC中,AB=10cm,BC=20cm,点P从A开始沿AB边向B点以1cm/s的速度移动,到达点B时停止.点Q从点B开始沿BC边向C点以2cm/s的速度移动,到达点C时停止.如果P、Q分别从A、B同时出发,经几秒种△PBQ与△ABC相似?
14. 如图,△ABC中,AB=10cm,BC=20cm,点P从A开始沿AB边向B点以1cm/s的速度移动,到达点B时停止.点Q从点B开始沿BC边向C点以2cm/s的速度移动,到达点C时停止.如果P、Q分别从A、B同时出发,经几秒种△PBQ与△ABC相似?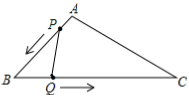 15. 如图,AB•AE=AD•AC,且∠1=∠2,求证:△ABC∽△ADE.
15. 如图,AB•AE=AD•AC,且∠1=∠2,求证:△ABC∽△ADE.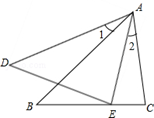 16. 已知:如图,在△ABC中,D,E分别为AB、AC边上的点,且AD= AE,连接DE.若AC=3,AB=5.求证:△ADE∽△ACB.
16. 已知:如图,在△ABC中,D,E分别为AB、AC边上的点,且AD= AE,连接DE.若AC=3,AB=5.求证:△ADE∽△ACB.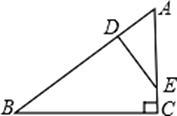 17. 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动)。如果P、Q分别从A、B两点同时出发,设运动时间为t秒。
17. 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动)。如果P、Q分别从A、B两点同时出发,设运动时间为t秒。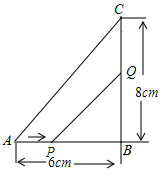 (1)、则:BQ=cm:BP=cm;(用含t的代数式表示)(2)、经过几秒钟,△PBQ的面积等于△ABC的三分之一?(3)、经几秒钟△PBQ与△ABC相似?试说明理由.
(1)、则:BQ=cm:BP=cm;(用含t的代数式表示)(2)、经过几秒钟,△PBQ的面积等于△ABC的三分之一?(3)、经几秒钟△PBQ与△ABC相似?试说明理由.