初中数学人教版2019-2020学年九年级上学期期中模拟试卷
试卷更新日期:2019-10-25 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
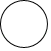 圆
B、
圆
B、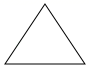 等边三角形
C、
等边三角形
C、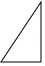 直角三角形
D、
直角三角形
D、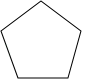 正五边形
2. 关于x的一元二次方程 (k为实数)根的情况是( )
正五边形
2. 关于x的一元二次方程 (k为实数)根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定3. 下列图形,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正五边形 C、等腰直角三角形 D、矩形4. 能说明命题“关于x的方程x2-4x+m=0一定有实数根”是假命题的反例为( )A、m=-1 B、m=0 C、m=4 D、m=55. 已知抛物线y=-x2+1,下列结论:①抛物线开口向上;②抛物线与x轴交于点(-1,0)和点(1,0);③抛物线的对称轴是y轴;④抛物线的顶点坐标是(0,1);⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.其中正确的个数有( )
A、5个 B、4个 C、3个 D、2个6. 下列函数中,y总随x的增大而减小的是( )A、y=4x B、y=﹣4x C、y=x﹣4 D、y=x27. 已知二次函数 (h为常数),在自变量 的值满足 的情况下,与其对应的函数值 的最大值为0,则 的值为( )A、 和 B、 和 C、 和 D、 和8. 在平面直角坐标系中,点 的坐标为 ,以原点为中心,将点 顺时针旋转 得到点 ,则点 的坐标为( )A、 B、 C、 D、9. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0),其对称轴为直线x= ,结合图象分析下列结论:
①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大;④一元二次方程cx2+bx+a=0的两根分别为x1= ,x2= ;⑤ <0;⑥若m,n(m<n)为方程a(x+3)(x-2)+3=0的两个根,则m<-3且n>2.其中正确的结论有( )
A、3个 B、4个 C、5个 D、6个10. 抛物线 ( 是常数), ,顶点坐标为 .给出下列结论:①若点 与点 在该抛物线上,当 时,则 ;②关于 的一元二次方程 无实数解,那么( )A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误11. 如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到 , 与BC,AC分别交于点D,E.设 , 的面积为 ,则 与 的函数图象大致为( )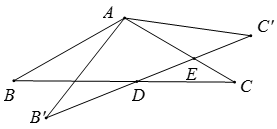 A、
A、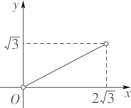 B、
B、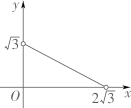 C、
C、 D、
D、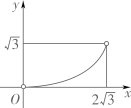 12. 已知 、 是一元二次方程 的两个实数根,下列结论错误的是( )A、 B、 C、 D、
12. 已知 、 是一元二次方程 的两个实数根,下列结论错误的是( )A、 B、 C、 D、二、填空题
-
13. 用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 .14. 如果点 , 在抛物线 上,那么 的值为;15. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
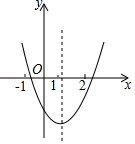 16. 如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.
16. 如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.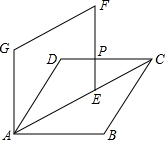
三、解答题
-
17. 解方程:(1)、2x2-13x+1 5=0(2)、18. 要组织一次篮球邀请比赛,参赛的队伍每两个队都要比赛一场.赛程安排7天,每天比赛4场,问组织者应该邀请多少个队参赛?19. 已知:在平面直角坐标系中, 的三个顶点的坐标分别为 , , .
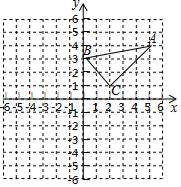
①画出 关于原点成中心对称的 ,并写出点 的坐标;
②画出将 绕点 按顺时针旋转 所得的 .
四、综合题
-
20. 在画二次函数 的图象时,甲写错了一次项的系数,列表如下
……
﹣1
0
1
2
3
……
……
6
3
2
3
6
……
乙写错了常数项,列表如下:
……
﹣1
0
1
2
3
……
……
﹣2
﹣1
2
7
14
……
通过上述信息,解决以下问题:
(1)、求原二次函数 的表达式;(2)、对于二次函数 ,当 时, 的值随 的值增大而增大;(3)、若关于 的方程 有两个不相等的实数根,求 的取值范围.21. 已知二次函数y=﹣x2+2mx﹣m2+4.(1)、求证:该二次函数的图象与x轴必有两个交点;(2)、若该二次函数的图象与x轴交于点A、B(点A在点B的左侧),顶点为C,①求△ABC的面积;
22. (感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”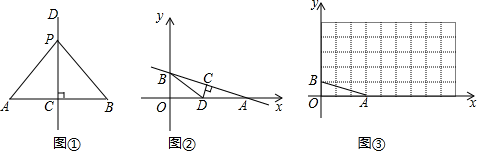
(探究)如图②,在平面直角坐标系中,直线y=- x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
(应用)如图③
(1)、将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;(2)、若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为.23. 如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).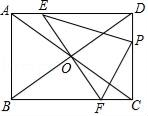 (1)、填空:PC= , FC=(用含x的代数式表示)(2)、求△PEF面积的最小值;(3)、在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.
(1)、填空:PC= , FC=(用含x的代数式表示)(2)、求△PEF面积的最小值;(3)、在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.