初中数学浙教版九年级上册4.3 相似三角形 同步训练
试卷更新日期：2019-10-25 类型：同步测试
一、基础夯实
-
1. 如图，△ABC~△DEF，相似比为1：2．若BC=1，则EF的长是（ ）
A、1 B、2 C、3 D、42. 若△ABC的每条边长增加各自的10%得△A'B'C' ， 则∠B'的度数与其对应角∠B的度数相比（ ）
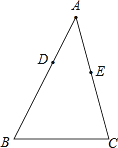
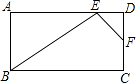
A、增加了10% B、减少了10% C、增加了（1+10%） D、没有变化3. 在△ABC和△DEF中，∠A=40°，∠D=60°，∠E=80°， ，那么∠B的度数是（ ）A、40° B、60° C、80° D、100°4. 如图，已知△ABC，D，E分别是AB，AC边上的点．AD=3cm，AB=8cm，AC=10cm．若△ADE∽△ABC，则AE的值为（ ）
A、 cm B、 cm或 cm C、 cm或 cm D、 cm5. 如图，△ABO∽△CDO，若BO＝6，DO＝3，CD＝2，则AB的长是（ ）
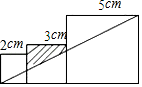
A、2 B、3 C、4 D、56. 已知△ABC∽△A′B′C′且S△ABC:S△A′B′C′＝1:2，则AB:A′B′＝ ．7. 如图，网高为0.8米，击球点到网的水平距离为3米，小明在打网球时，要使球恰好能打过网，且落点恰好在离网4米的位置上，则球拍击球的高度h为米.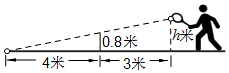
8. 如图中两三角形相似，则x= ．
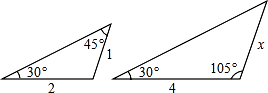9. △ABC的三边分别为 、 、2，△A′B′C′的两边长分别为2和2 ，如果△ABC∽△A′B′C′，那么△A′B′C′的第三边的长是 ．10. 如图，已知△AOB∽△DOC，OA=2，AD=9，OB=5，DC=12．求AB，OC的长．
二、强化提升
-
11. 要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为3cm， 和6m，另一个三角形的最长边长为12cm，则它的最短边长为A、6cm B、9cm C、16cm D、24cm12. 一个三角形三边的长分别为3,4,5,另一个与它相似的三角形的最长边是10,则其他两边的和是（ ）A、9 B、12 C、13 D、1413. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（ ）
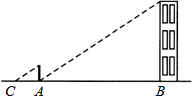A、10米 B、12米 C、15米 D、
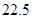米
14. 如图，△ABC中，点D在线段BC上，且△ABC∽△DBA，则下列结论一定正确的是（ ）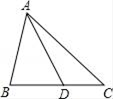
A、AB2=BC•BD B、AB2=AC•BD C、AB•AD=BD•BC D、AB•AD=AD•CD15. 如图，在△ABC中，点D，E分别在AB，AC上，且DE∥BC，AD=1，BD=2，那么 的值为（ ）
A、1：2 B、1：3 C、1：4 D、2：3
