初中数学浙教版九年级上册4.1 比例线段-黄金分割 同步训练
试卷更新日期:2019-10-25 类型:同步测试
一、基础巩固
-
1. 已知,C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=( )A、3﹣ B、 ( +1) C、 ﹣1 D、 ( ﹣1)2. 点C是线段AB的黄金分割点,且AB=6cm,则BC的长为( )cmA、
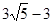 B、
B、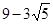 C、
C、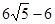 或
或 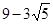 D、
D、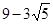 或
或 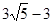 3. 主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是( )
3. 主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是( )①AB:AC=AC:BC;②AC≈6.18米;③AC=10( )米;④BC=10(3− )米或10( −1)米.
A、①②③④ B、①②③ C、①③ D、④4. 在长度为1的线段上找到两个黄金分割点P,Q,则PQ=( )A、 B、 C、 D、5. 已知 为线段 的黄金分割点,且 ,则( ).
A、 B、 C、 D、6. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为( )A、12.36 cm B、13.6 cm C、32.36 cm D、7.64 cm7. 若a:b=3:2,且b是a、c的比例中项,则b:c等于( )A、4:3 B、3:4 C、3:2 D、2:38. 已知线段a=4,b=9,线段x是a,b的比例中项,则x等于( )A、6 B、6或﹣6 C、﹣6 D、369. 若 ,请再写出一条线段的长,使它与a、b这三条线段中的一条是另外两条的比例中项,则这条线段长为 .
10. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为cm. 11. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m)
11. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m) 12. 已知线段a=0.3m,b=60cm,c=12dm.(1)、求线段a与线段b的比.(2)、如果线段a、b、c、d成比例,求线段d的长.(3)、b是a和c的比例中项吗?为什么?
12. 已知线段a=0.3m,b=60cm,c=12dm.(1)、求线段a与线段b的比.(2)、如果线段a、b、c、d成比例,求线段d的长.(3)、b是a和c的比例中项吗?为什么?二、提高特训
-
13. 点C为线段AB的黄金分割点,且AC>BC,下列说法正确的有( )
①AC= AB,②AC= AB,③AB:AC=AC:BC,④AC≈0.618AB
A、1个 B、2个 C、3个 D、4个14. “黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置( )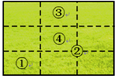 A、① B、② C、③ D、④15. 如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是( )
A、① B、② C、③ D、④15. 如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是( )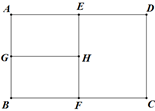 A、5个 B、4个 C、3个 D、2个16. 如图,在五角星中,AD=BC,且C、D两点都是AB的黄金分割点,CD=1,则AB的长是.
A、5个 B、4个 C、3个 D、2个16. 如图,在五角星中,AD=BC,且C、D两点都是AB的黄金分割点,CD=1,则AB的长是. 17. 如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 .(填“>”“=”或“<”)
17. 如图,已知 是线段 的黄金分割点,且 .若 表示以 为一边的正方形的面积, 表示长是 、宽是 的矩形的面积,则 .(填“>”“=”或“<”)