吉林省省考卷2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期：2019-10-25 类型：月考试卷
一、单项选择题(每小题2分，共12分)
-
1. 一个二次函数y=ax2+bx+c的图像如图所示，该二次函数二次项系数a的值可能是（ ）
A、-2 B、3 C、 D、2.32. 一元二次方程(x+3)2=16可转化为两个一元一次方程，其中一个一元次方程是x+3=4，则另一个一元一次方程是（ ）A、x-3=-4 B、x-3=4 C、x+3=4 D、x+3=-43. 用配方法解方程x2-2x-3=0时，原方程应变形为（ ）A、(x+1)2=4 B、(x-1)2=4 C、(x+2)2=7 D、(x-2)2=74. 抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线解析式是（ ）A、y=3(x-1)2-2 B、y=3(x+1)2-2 C、y=3(x+1)2+2 D、y=3(x-1)2+25. 已知二次函数y=ax2+bx+c的图像如图所示，那么根据图像，下列判断中不正确的是（ ）
A、a<0 B、b>0 C、c>0 D、abc>06. 光彩市场某个体商户购进某种电子产品的进价是50元/个，根据市场调研发现售价是80元/个时，每周可卖出160个.若销售价格每个降低2元，则每周可多卖出20个.若商户计划下周利润达到5200元，则此电子产品的售价为每个多少元?设销售价格每个降低x元(x为偶数)，则所列方程为（ ）A、(80-x)(160+20x)=5200 B、(30-x)(160+20x)=5200 C、(30-x)(160+10x)=5200 D、(50-x)(160+10x)=5200二、填空题(每小题3分，共24分)
-
7. 一元二次方程x2-3x+1=0的根的判别式的值是 。8. 二次函数y=-6(x-5)2+8的图像的顶点坐标是 。9. 方程3x2-x=0的解为。10. 若关于 的一元二次方程 有实数根，则 的值可以为（写出一个即可）．11. 抛物线y=x2-2在y轴右侧的部分是的。（填“上升”或“下降”）12. 已知二次函数y=2(x-1)2的图像如图所示，则△ABO的面积是 。
13. 如图是二次函数y=ax2+bx+c的图像，已知点(2，y1)，(3，y2)是函数图象上的两个点，则y1 ， y2的大小关系是。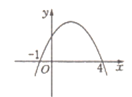
14. 如图，在平面直角坐标系中，抛物线y=(x-2)2与x轴交于点A，与y轴交于点B，过点B作BC∥x轴，交抛物线于点C，过点A作AD∥y轴，交BC于点D，点P在BC下方的抛物线上(不与点B，C重合)，连接PC，PD，设△PCD的面积为S，则S的取值范围是。
三、解答题(每小题5分，共20分)
-
15. 解方程：x2-6x-1=016. 解方程：(x+1)2=4(x+1)17. 若二次函数图象的顶点坐标是(2，1)，且经过点(1，-2)，求此二次函数的解析式。18. 小明在解方程x2-2x-1=0时出现了错误，其解答过程如下：
解：x2-2x=-1（第一步）
x2-2x+1=-1+1（第二步）
(x-1)2=0（第三步）
x1=x2=1（第四步）
(1)、小明解答过程是从第步开始出错的，其错误原因是；(2)、请写出此题正确的解答过程。四、解答题(每小题7分，共28分)
-
19. 已知关于x的方程x2-2x+2m-1=0有实数根，且m为正整数，求m的值及此时方程的根。20. 已知二次函数y=-x2+2x-1.
(1)、直接写出抛物线的顶点坐标(2)、如图，在平面直角坐标系xOy内作出二次函数y=-x2+2x-1的草图(3)、直接写出x取什么值时，函数的值y随x的增大而增大?21. 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业。据统计，目前广东5G基站的数量约1.5万座，计划到2020年年底，全省5G基站数量是目前的4倍，到2022年年底，全省5G基站数量将达到17.34万座。(1)、计划到2020年年底，全省5G基站的数量是多少万座?(2)、按照计划，求2020年年底到2022年年底，全省5G基站数量的年平均增长率。22. 某地计划对矩形广场进行扩建改造.如图，原广场长50m，宽40m，要求扩充后的矩形广场长与宽的比为3：2.扩充区域的扩建费用为每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用为每平方米100元，如果计划总费用为642000那么扩充后广场的长和宽应分别是多少米?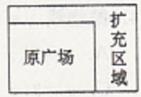
五、解答题(每小题8分，共16分)
-
23. 如图，抛物线y=-x2+bx+c经过点A(4，0)和点B(0，2)，且抛物线的对称轴为直线l，顶点为C.
(1)、求抛物线的解析式；(2)、连接AC，BC，BD，求四边形ADBC的面积24. 如图，在平面直角坐标系中，抛物线y=ax2-2x+ (a>0)与y轴交于点A，过点A作x轴的平行线交抛物线于点M，P为抛物线的顶点，直线OP交直线AM于点B，且M为线段AB的中点。
(1)、求抛物线的对称轴及点M坐标(2)、求直线OP的解析式(3)、求抛物线的解析式。六、解答题(每小题10分，共20分)
-
25. 如图，矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动.已知P，Q分别从A，B同时出发
(1)、几秒后，△PBQ的面积等于9cm2?(2)、点P与点Q之间的距离可能为5cm吗?说明理由(3)、几秒后，五边形 APQCD的面积最小?最小值是多少?26. 如图
(1)、如图①，函数y=x+1在-1≤x≤2内的图像的最高点与最低点的纵坐标之差为。(2)、如图②，函数y=x2在-1≤x≤2内的图像的最高点与最低点的纵坐标之差为 。(3)、如图③，函数y=x2-1在-1≤x≤a内的图像的最高点与最低点的纵坐标之差为 ，求a的值。(4)、如图④，函数y=x2-4x-1在1≤x≤c内的图像的最高点与最低点的纵坐标之差为h，直接写出h与c的函数关系式，并写出自变量c的取值范围。