初中数学华师大版八年级上学期 第13章 13.3.1 等腰三角形的性质
试卷更新日期:2019-10-24 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
 A、40° B、45° C、50° D、60°2. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )
A、40° B、45° C、50° D、60°2. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )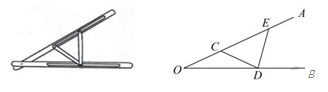 A、60° B、65° C、75° D、80°3. 如图,△ABC中,AC=BC<AB.若∠1、∠2分别为∠ABC、∠ACB的外角,则下列角度关系何者正确( )
A、60° B、65° C、75° D、80°3. 如图,△ABC中,AC=BC<AB.若∠1、∠2分别为∠ABC、∠ACB的外角,则下列角度关系何者正确( ) A、 B、 C、 D、4. 如图,在△ABC中,点D是BC边上一点,AD=AC,过点D作DE⊥BC交AB于E,若△ADE是等腰三角形,则下列判断中正确的是( )
A、 B、 C、 D、4. 如图,在△ABC中,点D是BC边上一点,AD=AC,过点D作DE⊥BC交AB于E,若△ADE是等腰三角形,则下列判断中正确的是( ) A、∠B=∠CAD B、∠BED=∠CAD C、∠ADB=∠AED D、∠BED=∠ADC5. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍
A、∠B=∠CAD B、∠BED=∠CAD C、∠ADB=∠AED D、∠BED=∠ADC5. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍二、填空题
-
6. 在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠EPF=147°,则∠PFE的度数是 。
 7. 等腰△ABC中,BD⊥AC,垂足为点D,且BD= AC,则等腰△ABC底角的度数为 .8. 在 中,AB=AC, ,则 :∠B=。
7. 等腰△ABC中,BD⊥AC,垂足为点D,且BD= AC,则等腰△ABC底角的度数为 .8. 在 中,AB=AC, ,则 :∠B=。
9. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.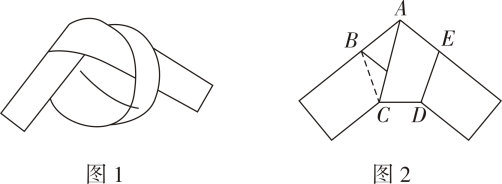 10. 如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC与点D,连结AD,若∠B=40°,∠C=36°,则∠DAC的度数是.
10. 如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC与点D,连结AD,若∠B=40°,∠C=36°,则∠DAC的度数是.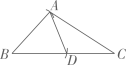
三、综合题