2017年江西省赣州市高考数学二模试卷（理科）

试卷更新日期：2017-07-07 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知复数z满足（1﹣i）²•z=1+2i，则在复平面内复数 $\bar{z}$ 对应的点为（）

A、 $(- 1 ， - \frac{1}{2})$ B、 $(1 ， - \frac{1}{2})$ C、 $(- \frac{1}{2} ， 1)$ D、 $(- \frac{1}{2} ， - 1)$

查看试题解析
2. 已知集合P={x|x²﹣2x﹣8≤0}，Q={x|x≥a}，（∁_RP）∪Q=R，则a的取值范围是（）

A、（﹣2，+∞） B、（4，+∞） C、（﹣∞，﹣2] D、（﹣∞，4]

查看试题解析
3. 对于下列说法正确的是（）

A、若f（x）是奇函数，则f（x）是单调函数 B、命题“若x²﹣x﹣2=0，则x=1”的逆否命题是“若x≠1，则x²﹣x﹣2=0” C、命题p：∀x∈R，2^x＞1024，则￢p：∃x₀∈R， $2^{x_{0}} < 1024$ D、命题“∃x∈（﹣∞，0），2^x＜x²”是真命题

查看试题解析
4. 如图，ABCD是以O为圆心、半径为2的圆的内接正方形，EFGH是正方形ABCD的内接正方形，且E、F、G、H分别为AB、BC、CD、DA的中点．将一枚针随机掷到圆O内，用M表示事件“针落在正方形ABCD内”，N表示事件“针落在正方形EFGH内”，则P（N|M）=（）

A、 $\frac{1}{π}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
5. 函数 $f (x) = \frac{1 + e^{2 x}}{1 - e^{2 x}} \cdot x$ （其中e是自然对数的底数）的大致图象为（）

A、 B、 C、 D、

查看试题解析
6. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ 的离心率为 $\sqrt{5}$ ，则抛物线x²=4y的焦点到双曲线的渐近线的距离是（）

A、 $\frac{\sqrt{5}}{10}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
7. 正方体ABCD﹣A₁B₁C₁D₁的棱长为1，点E，F分别是棱D₁C₁ ， B₁C₁的中点，过E，F作一平面α，使得平面α∥平面AB₁D₁ ，则平面α截正方体的表面所得平面图形为（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
8. 执行如图所示的程序框图，若输入的a=16，b=4，则输出的n=（）

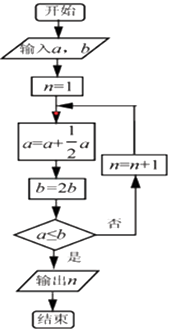A、4 B、5 C、6 D、7

查看试题解析
9. 已知公差不为0的等差数列{a_n}与等比数列 ${b_{n}} ， a_{1} = 2 ， b_{n} = a_{2^{n}}$ ，则{b_n}的前5项的和为（）

A、142 B、124 C、128 D、144

查看试题解析
10. 如图所示，为了测量A，B处岛屿的距离，小明在D处观测，A，B分别在D处的北偏西15°、北偏东45°方向，再往正东方向行驶40海里至C处，观测B在C处的正北方向，A在C处的北偏西60°方向，则A，B两处岛屿间的距离为（）

A、 $20 \sqrt{6}$ 海里 B、 $40 \sqrt{6}$ 海里 C、 $20 (1 + \sqrt{3})$ 海里 D、40海里

查看试题解析
11. 已知动点A（x_A ， y_A）在直线l：y=6﹣x上，动点B在圆C：x²+y²﹣2x﹣2y﹣2=0上，若∠CAB=30°，则x_A的最大值为（）

A、2 B、4 C、5 D、6

查看试题解析
12. 已知函数f（x）=x+e^x^﹣^a ， $g (x) = \frac{1}{2} 1 n (2 x + 1) - 4 e^{a - x}$ ，其中e为自然对数的底数，若存在实数x₀ ，使f（x₀）﹣g（x₀）=4成立，则实数a的值为（）

A、n2﹣1 B、1﹣1n2 C、1n2 D、﹣1n2

查看试题解析

二、填空题

13. 已知向量 $\vec{a}$ =（1，﹣2）， $\vec{a}$ ⊥ $\vec{b}$ ，|2 $\vec{a}$ ﹣ $\vec{b}$ |=5，则| $\vec{b}$ |= ．

查看试题解析
14. 若 $(1 + y^{3}) {(x - \frac{1}{x^{2} y})}^{n} (n \in N_{+})$ 的展开式中存在常数项，则常数项为．

查看试题解析
15. 某多面体的三视图如图所示，则该多面体外接球的体积为．

查看试题解析
16. 如图所示，由直线x=a，x=a+1（a＞0），y=x²及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间，即 $a^{2} < \int_{a}^{a + 1} x^{2} d x < {(a + 1)}^{2}$ ．类比之，若对∀n∈N₊ ，不等式 $\frac{k}{n + 1} + \frac{k}{n + 2} + \dots + \frac{k}{2 n} < 1 n 4 < \frac{k}{n} + \frac{k}{n + 1} + \dots + \frac{k}{2 n - 1}$ 恒成立，则实数k等于．

查看试题解析

三、解答题

17. 已知函数f（x）=sinωxcosωx﹣ $\sqrt{3} c o s^{2} ω x + \frac{\sqrt{3}}{2}$ （ω＞0）图象的两条相邻对称轴为 $\frac{π}{2}$ ．

(1)、求函数y=f（x）的对称轴方程；

(2)、若函数y=f（x）﹣ $\frac{1}{3}$ 在（0，π）上的零点为x₁ ， x₂ ，求cos（x₁﹣x₂）的值．

查看试题解析
18. 某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：

(1)、记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；

(2)、若购进这批小龙虾100千克，试估计这批小龙虾的数量；

(3)、为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
等级
一等品
二等品
三等品
重量（g）
[5，25）
[25，45）
[45，55]
按分层抽样抽取10只，再随机抽取3只品尝，记X为抽到二等品的数量，求抽到二级品的期望．

查看试题解析
19. 如图，五面体ABCDE中，四边形ABDE是菱形，△ABC是边长为2的正三角形，∠DBA=60°， $C D = \sqrt{3}$ ．

(1)、证明：DC⊥AB；

(2)、若点C在平面ABDE内的射影H，求CH与平面BCD所成的角的正弦值．

查看试题解析
20.
如图，椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $e = \frac{\sqrt{3}}{2}$ ，顶点为A₁、A₂、B₁、B₂ ，且 $\vec{A_{1} B_{1}} \cdot \vec{A_{1} B_{2}} = 3$ ．

(1)、求椭圆C的方程；

(2)、P是椭圆C上除顶点外的任意点，直线B₂P交x轴于点Q，直线A₁B₂交A₂P于点E．设A₂P的斜率为k，EQ的斜率为m，试问2m﹣k是否为定值？并说明理由．

查看试题解析
21. 已知函数f（x）=x²﹣x，g（x）=e^x﹣ax﹣1（e为自然对数的底数）．

(1)、讨论函数g（x）的单调性；

(2)、当x＞0时，f（x）≤g（x）恒成立，求实数a的取值范围．

查看试题解析
22. 在直角坐标系xOy中，直线 $l ： {\begin{matrix} x = t c o s α \\ y = t s i n α \end{matrix}$ （t为参数， $α \in (0 ， \frac{π}{2})$ ）与圆C：x²+y²﹣2x﹣4x+1=0相交于点A，B，以O为极点，x轴正半轴为极轴建立极坐标系．

(1)、求直线l与圆C的极坐标方程；

(2)、求 $\frac{1}{| O A |} + \frac{1}{| O B |}$ 的最大值．

查看试题解析
23. 已知函数f（x）=m﹣|2﹣x|，且f（x+2）＞0的解集为（﹣1，1）．

(1)、求m的值；

(2)、若正实数a，b，c，满足a+2b+3c=m．求 $\frac{1}{a} + \frac{1}{2 b} + \frac{1}{3 c}$ 的最小值．

查看试题解析

等级	一等品	二等品	三等品
重量（g）	[5，25）	[25，45）	[45，55]