2016-2017学年浙江省杭州市经济开发区四校七年级下学期期中数学试卷

试卷更新日期：2017-07-07 类型：期中考试

进入出卷网下载

一、选择题

1. 如图，直线b、c被直线a所截，则∠1与∠2是（）

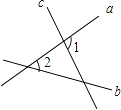A、同位角 B、内错角 C、同旁内角 D、对顶角

查看试题解析
2. 下列计算正确的是（　　）

A、a³+a⁴=a⁷ B、（a³）⁴=a⁷ C、（﹣a²b³）³=a⁶b⁹ D、2a⁴•3a⁵=6a⁹

查看试题解析
3. 二元一次方程2x+y=7的正整数解有多少组（）

A、2 B、3 C、5 D、4

查看试题解析
4. 如图，将一条两边沿互相平行的纸带按图折叠，则∠α的度数等于（）

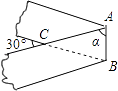A、50° B、60° C、75° D、85°

查看试题解析
5. 已知﹣2xⁿ^﹣^3my³与3x⁷y^m+n是同类项，则mⁿ的值是（　　）

A、4 B、1 C、﹣4 D、﹣1

查看试题解析
6. 若将一副三角板按如图所示的方式放置，则下列结论不正确的是（）

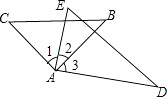A、∠1=∠3 B、如果∠2=30°，则有AC∥DE C、如果∠2=30°，则有BC∥AD D、如果∠2=30°，必有∠4=∠C

查看试题解析
7. 若（x²+px+q）（x﹣2）展开后不含x的一次项，则p与q的关系是（　　）

A、p=2q B、q=2p C、p+2q=0 D、q+2p=0

查看试题解析
8. 父子二人并排垂站立于游泳池中时，爸爸露出水面的高度是他自身身高的 $\frac{1}{3}$ ，儿子露出水面的高度是他自身身高的 $\frac{1}{7}$ ，父子二人的身高之和为3.2米．若设爸爸的身高为x米，儿子的身高为y米，则可列方程组为（）

A、 ${\begin{matrix} x + y = 3.2 \\ (1 + \frac{1}{7}) x = (1 + \frac{1}{3}) y \end{matrix}$ B、 ${\begin{matrix} x + y = 3.2 \\ (1 - \frac{1}{7}) x = (1 - \frac{1}{3}) y \end{matrix}$ C、 ${\begin{matrix} x + y = 3.2 \\ \frac{1}{3} x = \frac{1}{7} y \end{matrix}$ D、 ${\begin{matrix} x + y = 3.2 \\ (1 - \frac{1}{3}) x = (1 - \frac{1}{7}) y \end{matrix}$

查看试题解析
9. 有若干张面积分别为a²、b²、ab的正方形和长方形纸片，小明从中抽取了1张面积为b²的正方形纸片，6张面积为ab的长方形纸片．若他想拼成一个大正方形，则还需要抽取面积为a²的正方形纸片（　　）

A、4张 B、8张 C、9张 D、10张

查看试题解析
10. 已知关于x、y的二元一次方程组 $\{\begin{matrix} 3 x + 5 y = 6 \\ 3 x + k y = 10 \end{matrix}$ 给出下列结论：①当k=5时，此方程组无解；②若此方程组的解也是方程6x+15y=16的解，则k=10；③无论整数k取何值，此方程组一定无整数解（x、y均为整数），其中正确的是（　　）

A、①②③ B、①③ C、②③ D、①②

查看试题解析

二、填空题

11. 随着电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.000 000 7（毫米²），这个数用科学记数法表示为．

查看试题解析
12. 如图，直线l₁∥l₂ ， ∠α=∠β，∠1=35°，则∠2=°．

查看试题解析
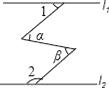13. 已知关于x、y的方程组 ${\begin{matrix} x + 2 y = 1 - a \\ x - y = 2 a - 5 \end{matrix}$ ，则代数式2^2x•4^y= ．

查看试题解析
14. 如图所示，与∠A是同旁内角的角共有个．

查看试题解析
15. 有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为．

查看试题解析
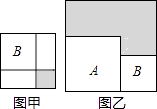16. 若x²+5x+8=a（x+1）²+b（x+1）+c，则a= ， b= ， c= ．

查看试题解析
17. 如果：（ka^m^﹣ⁿb^m⁺ⁿ）⁴=16a⁸b¹⁶ ，则k+m+n= ．

查看试题解析
18. 若（ $\frac{1}{2}$ t﹣1）^t^﹣²=1，则t可以取的值是．

查看试题解析
19. 一个自然数若能表示为两个自然数的平方差，则这个自然数称为“智慧数”．比如：2²﹣1²=3，则3就是智慧数；2²﹣0²=4，则4就是智慧数．

(1)、从0开始第7个智慧数是；

(2)、不大于200的智慧数共有．

查看试题解析

三、解答题

20. 计算题

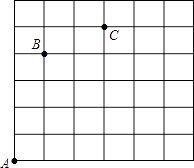
(1)、计算：| $\sqrt{3}$ ﹣2|+（ $\frac{1}{2}$ ）^﹣¹﹣（π﹣3.14）⁰﹣ $\sqrt[3]{27}$ ；

(2)、计算：[xy（3x﹣2）﹣y（x²﹣2x）]÷x²y．

查看试题解析
21. 解方程

(1)、 ${\begin{matrix} - \frac{1}{2} x + \frac{3}{4} y = 1 \\ - 2 x + y = - 8 \end{matrix}$

(2)、 ${\begin{matrix} 2 (2 x + 1) = y + 2 \\ 2 (y + 2) - 3 (2 x + 1) = 3 \end{matrix}$ ．

查看试题解析
22. 若在方格（每小格正方形边长为1m）上沿着网格线平移，规定：沿水平方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿竖直方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．例如：点A按“平移量”{1，4}可平移至点B．

(1)、从点C按“平移量”{ ， }可平移到点B；

(2)、若点B依次按“平移量”{4，﹣3}、{﹣2，1}平移至点D，
①请在图中标出点D；（用黑色水笔在答题卡上作出点D）
②如果每平移1m需要2.5秒，那么按此方法从点B移动至点D需要多少秒？
③观察点D的位置，其实点B也可按“平移量”{ ， }直接平移至点D；观察这两种平移的“平移量”，猜想：点E依次按“平移量”{2a，3b}、{﹣5a，b}、{a，﹣5b}平移至点F，则相当于点E按“平移量”{ ， }直接平移至点F．

查看试题解析
23. 如图，已知DC∥FP，∠1=∠2，∠FED=28°，∠AGF=80°，FH平分∠EFG．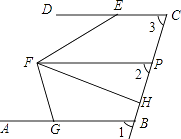

(1)、说明：DC∥AB；

(2)、求∠PFH的度数．

查看试题解析
24. 小明家需要用钢管做防盗窗，按设计要求，其中需要长为0.8m，2.5m且粗细相同的钢管分别为100根，32根，并要求这些用料不能是焊接而成的．现钢材市场的这种规格的钢管每根为6m．

(1)、试问一根6m长的圆钢管有哪些裁剪方法呢？请填写下空（余料作废）．
方法①：当只裁剪长为0.8m的用料时，最多可剪根；
方法②：当先剪下1根2.5m的用料时，余下部分最多能剪0.8m长的用料根；
方法③：当先剪下2根2.5m的用料时，余下部分最多能剪0.8m长的用料根．

(2)、分别用（1）中的方法②和方法③各裁剪多少根6m长的钢管，才能刚好得到所需要的相应数量的材料？

(3)、试探究：除（2）中方案外，在（1）中还有哪两种方法联合，所需要6m长的钢管与（2）中根数相同？

查看试题解析