2016-2017学年江西省宜春市高安市七年级下学期期中数学试卷

试卷更新日期：2017-07-07 类型：期中考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，点M（﹣2，3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列式子正确的是（）

A、 $\sqrt[3]{- 7}$ =﹣ $\sqrt[3]{7}$ B、 $\pm \sqrt{49}$ =7 C、 $\sqrt{25}$ =±5 D、 $\sqrt{{(- 3)}^{2}}$ =﹣3

查看试题解析
3. 如图，AB∥CD，直线l交AB于点E，交CD于点F，若∠2=80°，则∠1等于（）

A、120° B、110° C、100° D、80°

查看试题解析
4. 如图，直线l₁、l₂被直线l₃、l₄所截，下列条件中，不能判断直线l₁∥l₂的是（）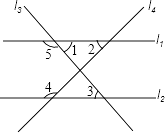

A、∠1=∠3 B、∠5=∠4 C、∠5+∠3=180° D、∠4+∠2=180°

查看试题解析
5. 线段CD是由线段AB平移得到的．点A（﹣1，4）的对应点为C（4，7），则点B（﹣4，﹣1）的对应点D的坐标为（　　）

A、（2，9） B、（5，3） C、（1，2） D、（﹣9，﹣4）

查看试题解析
6. 如图是某公园里一处矩形风景欣赏区ABCD，长AB=50米，宽BC=25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（）

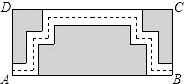A、100米 B、99米 C、98米 D、74米

查看试题解析

二、填空题

7. 已知点P的坐标为（5，﹣12），则点P到x轴的距离为．

查看试题解析
8. 已知一个正数的两个平方根分别是3a+2和a+14，则这个正数是．

查看试题解析
9. 如图，在数轴上1， $\sqrt{2}$ 的对应点分别是A、B，A是线段BC的中点，则点C所表示的数是．

查看试题解析
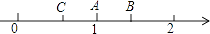10. 如图，已知AB、CD相交于点O，OE⊥AB，∠EOC=28°，则∠AOD=度．

查看试题解析
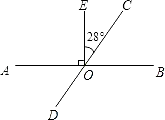11. 已知|a﹣27|与（b+8）²互为相反数，则 $\sqrt[3]{a}$ + $\sqrt[3]{b}$ = ．

查看试题解析
12. 如图所示：图象中所反映的过程是：小冬从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x轴表示时间，y轴表示小冬离家的距离．根据图象提供的信息，下列说法正确的有
①体育场离小冬家2.5千米 ②小冬在体育场锻炼了15分钟
③体育场离早餐店4千米 ④小冬从早餐店回家的平均速度是3千米/小时．

查看试题解析

三、解答题

13. 计算题

(1)、计算： $\sqrt{\frac{4}{9}}$ ﹣ $\sqrt{{(- 2)}^{4}}$ + $\sqrt[3]{\frac{19}{27} - 1}$ ﹣（﹣1）²⁰¹⁷

(2)、求满足条件的x值：（x﹣1）²=9．

查看试题解析
14. 已知x﹣2的平方根是±2， $\sqrt[3]{2 x + y + 7}$ =3，求x²+y²的平方根．

查看试题解析
15. 完成下面推理过程：
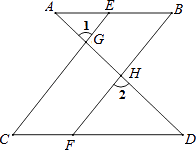
如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
∵∠1=∠2（已知），
且∠1=∠CGD（），
∴∠2=∠CGD（等量代换）．
∴CE∥BF（）．
∴∠ =∠C（）．
又∵∠B=∠C（已知），
∴∠ =∠B（等量代换）．
∴AB∥CD（）．

查看试题解析
16. 实数a，b在数轴上的位置如图所示．化简： $\sqrt{a^{2}}$ + $\sqrt{b^{2}}$ + $\sqrt{{(a + 1)}^{2}}$ + $\sqrt{{(b - 1)}^{2}}$ ．

查看试题解析
17. 如图，AB∥CD，AD⊥AC，垂足为点A，∠ADC=32°，求∠CAB的度数．

查看试题解析
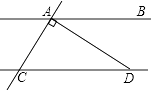18. 刘聪和爸爸、妈妈到人民公园游玩，回到家后，他利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴．y轴．只知道游乐园D的坐标为（2，﹣2），请你帮她画出平面直角坐标系，并写出其他各景点A、B、C、E、F的坐标．

查看试题解析
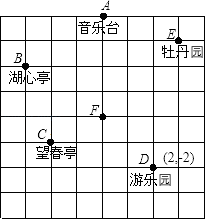19. 如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．请你判断AD和BE的位置关系，并说明理由．

查看试题解析
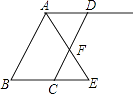20. 如图，直线AB、CD相交于O点，∠AOC与∠AOD的度数比为4：5，OE⊥AB，OF平分∠DOB，求∠EOF的度数．

查看试题解析
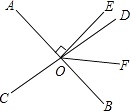21. 如图，∠AGF=∠ABC，∠1+∠2=180°，

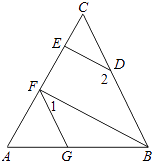(1)、求证；BF∥DE．

(2)、如果DE垂直于AC，∠2=150°，求∠AFG的度数．

查看试题解析
22.
如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形，建立如图所示的平面直角坐标系，已知点A（1，0），B（4，0），C（3，3），D（1，4）

(1)、描出A、B、C、D、四点的位置，并顺次连接ABCD，

(2)、四边形ABCD的面积是．

(3)、把四边形ABCD向左平移5个单位，再向下平移2个单位得到四边形A'B'C'D'，写出点A'、B'、C'、D'的坐标．

查看试题解析
23.
探索发现：
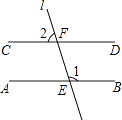
如图1，已知直线l₁∥l₂ ，且l₃和l₁、l₂分别相交于A、B两点，l₄和l₁、l₂分别交于C、D两点，∠ACP记作∠1，∠BDP记作∠2，∠CPD记作∠3．点P在线段AB上．

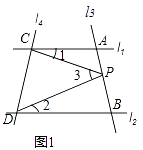(1)、若∠1=20°，∠2=30°，请你求出∠3的度数．

(2)、请你根据上述问题，请你找出图1中∠1、∠2、∠3之间的数量关系，并直接写出你的结论．

(3)、应用（2）中的结论解答下列问题：如图2，点A在B的北偏东 40°的方向上，在C的北偏西45°的方向上，请你根据上述结论直接写出∠BAC的度数．
拓展延伸：

(4)、
如果点P在直线l₃上且在A、B两点外侧运动时，其他条件不变，试探究∠1、∠2、∠3之间的关系（点P和A、B两点不重合），写出你的结论并说明理由．

查看试题解析