2016-2017学年江西省景德镇市昌江区七年级下学期期中数学试卷
试卷更新日期:2017-07-07 类型:期中考试
一、选择题
-
1. 下列计算中正确的是( )A、a3•a2=a6 B、(a3)2=a9 C、a6÷a6=0 D、a3+a3=2a32. 如图中,∠1和∠2是同位角的是( )A、
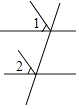 B、
B、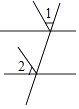 C、
C、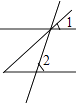 D、
D、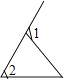 3. 若(x﹣5)(x+2)=x2+px+q,则p、q的值是( )A、3,10 B、﹣3,﹣10 C、﹣3,10 D、3,﹣104. 如图,下列能判定AB∥CD的条件有( )个.
3. 若(x﹣5)(x+2)=x2+px+q,则p、q的值是( )A、3,10 B、﹣3,﹣10 C、﹣3,10 D、3,﹣104. 如图,下列能判定AB∥CD的条件有( )个.①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
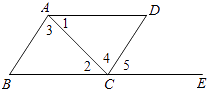 A、1 B、2 C、3 D、45. 下列计算正确的个数是( )
A、1 B、2 C、3 D、45. 下列计算正确的个数是( )①(x+y)2=x2+y2;
②(x+2y)(x﹣2y)=x2﹣2y2;
③(﹣x+y)2=x2﹣2xy+y2;
④(﹣a+b)(a﹣b)=a2﹣b2;
⑤(﹣2a﹣3)(2a﹣3)=9﹣4a2;
⑥(a﹣b)2=a2﹣b2 .
A、4个 B、3个 C、2个 D、1个6. “龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点、用s1、s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( )A、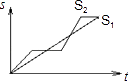 B、
B、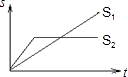 C、
C、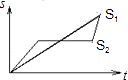 D、
D、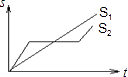
二、填空题
-
7. 计算:(﹣2a)3= .8. 甲型H1N1流感病毒的直径大约是0.000 000 081米,用科学记数法可表示为 .9. 某下岗职工购进一批货物,到集贸市场零售,已知卖出去的货物数量x与售价y的关系如下表:
数量x(千克)
1
2
3
4
5
售价y(元)
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
写出用x表示y的公式是 .
10. 如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明从学校回家的平均速度为千米∕小时.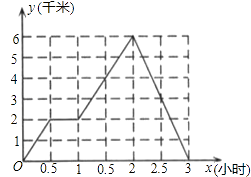 11. 若(3x+a)(x﹣2)的乘积中不含x一次项,则a= .12. 已知2a=5,2b=10,2c=50,那么a,b,c之间满足的等量关系是 .13. 如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2=度.
11. 若(3x+a)(x﹣2)的乘积中不含x一次项,则a= .12. 已知2a=5,2b=10,2c=50,那么a,b,c之间满足的等量关系是 .13. 如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2=度. 14. 一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发小时,快车追上慢车行驶了千米,快车比慢车早小时到达B地.
14. 一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发小时,快车追上慢车行驶了千米,快车比慢车早小时到达B地.
三、解答题
-
15. 计算题(1)、|﹣3|+(﹣1)2013×(π﹣3)0﹣(﹣ )﹣3(2)、a3•a3+(2a3)2+(﹣a2)3 .16. 先化简,再求值;(2m﹣1)2﹣(3m+1)(3m﹣1)+5m(m﹣1),其中m= .17. 已知a+b=5,ab=7,求下列代数式的值:(1)、(2)、a2﹣ab+b2 .18. 推理填空:
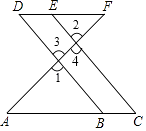
完成下列证明:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.
试说明:AC∥DF
解:∵∠1=∠2,(已知)
∠1=∠3()
∴∠2=∠3,(等量代换)
∴∥ , ()
∴∠C=∠ABD,()
又∵∠C=∠D,(已知)
∴∠D=∠ABD,()
∴AC∥DF.()
 19. 如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=2a,BC=3b,且E为AB边的中点,DF= BC,现打算在阴影部分种植一片草坪,求这片草坪的面积.
19. 如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=2a,BC=3b,且E为AB边的中点,DF= BC,现打算在阴影部分种植一片草坪,求这片草坪的面积.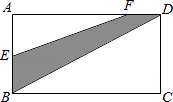 20. 已知: ,求x的值.21. 如图,直线CD与直线AB相交于点C,根据下列语句画图(注:可利用三角尺画图,但要保持图形清晰)
20. 已知: ,求x的值.21. 如图,直线CD与直线AB相交于点C,根据下列语句画图(注:可利用三角尺画图,但要保持图形清晰)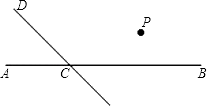 (1)、过点P作PQ∥AB,交CD于点Q,过点P作PR⊥CD,垂足为R;(2)、若∠DCB=120°,则∠QRC是多少度?并说明理由.22. 如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.问CD与AB有什么关系?并说明理由.
(1)、过点P作PQ∥AB,交CD于点Q,过点P作PR⊥CD,垂足为R;(2)、若∠DCB=120°,则∠QRC是多少度?并说明理由.22. 如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.问CD与AB有什么关系?并说明理由.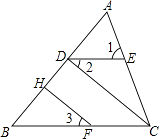 23. 如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.
23. 如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.下面提供三种思路:
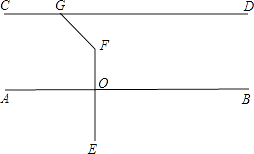 (1)、过点F作FH∥AB;(2)、延长EF交CD于M;(3)、延长GF交AB于K.
(1)、过点F作FH∥AB;(2)、延长EF交CD于M;(3)、延长GF交AB于K.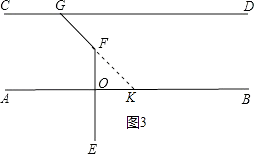
请你利用三个思路中的两个思路,将图形补充完整,求∠EFG的度数.
解(一):
解(二):
24. 如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF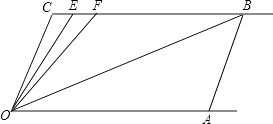 (1)、求∠EOB的度数;(2)、若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值(3)、在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
(1)、求∠EOB的度数;(2)、若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值(3)、在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.