2016-2017学年江苏省常州市七年级下学期期中数学试卷
试卷更新日期：2017-07-07 类型：期中考试
一、选择题
-
1. 下列图形中，可以由其中一个图形通过平移得到的是（ ）A、
B、
C、
D、
2. 一种病毒的长度约为0.00000432毫米，数据0.000000432用科学记数法表示为（ ）A、432×10﹣8 B、4.32×10﹣7 C、4.32×10﹣6 D、0.432×10﹣53. 下列计算正确的是（ ）A、（x3）2=x6 B、（﹣2x3）2=4x5 C、x4•x4=2x4 D、x5÷x=x54. 下列说法正确的是（ ）A、两直线平行，同旁内角可能相等 B、同底数幂相乘，底数相乘，指数相加 C、一个图形和它经过平移所得的图形中，两组对应点的连线一定平行 D、任何数的0次幂等于15. 若一个多边形的每个内角都为144°，则这个多边形是（ ）A、七边形 B、八边形 C、九边形 D、十边形6. 如图，直线l1∥l2 ， 直线l3与l1 ， l2分别交于A，B两点，点C是直线l2上一点，且AC⊥AB，若∠1=42°，则∠2的度数是（ ）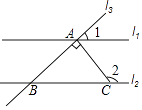
A、142° B、138° C、132° D、48°7. 若等腰三角形的两条边的长分别为3和1，则该等腰三角形的周长为（ ）A、5 B、7 C、5或7 D、无法确定8. 22017+32018的计算结果的末位数字是（ ）A、7 B、5 C、3 D、1二、填空题
-
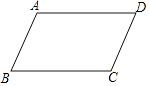
9. （﹣a）5÷（﹣a）3= ．10. 分解因式：2x2﹣8y2= ．11. 若x+y=3，则2x•2y的值为 ．12. 比较大小2﹣ ﹣ ．（填“＞”、“=”、“＜”）13. 如图，四边形ABCD中，AB∥CD，∠B=60°，当∠D=°时，AD∥BC．
14. 如图，AD是△ABC的中线，将△ABC沿射线BC方向平移2cm得到△EDF，则DC的长为 cm．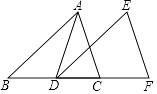
15. 已知m+n=﹣3，mn=5，则（2﹣m）（2﹣n）的值为 ．16. 若4x2﹣kx+9（k为常数）是完全平方式，则k= ．17. 已知△ABC的两条边的长度分别为3cm，6cm，若△ABC的周长为偶数，则第三条边的长度是 cm．18. 如图，直角三角板内部三角形的一个顶点恰好在直线a上（三角板内部三角形的三边分别与三角板的三边平行），若∠2=30°，∠3=50°，则∠1=°．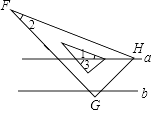
三、解答题
-
19. 计算(1)、（﹣2）﹣2﹣（ ）0+（﹣ ）2(2)、am+1•a+（﹣a）2•am（m是整数）(3)、（x﹣y）（x+y）﹣（x﹣y）2(4)、（x﹣1）（x2﹣1）（x+1）20. 因式分解：(1)、ab2﹣ba2(2)、a4﹣1(3)、（a﹣b）（5a+2b）﹣（a+6b）（a﹣b）(4)、x4﹣18x2+81．21. 求代数式x（2x﹣1）﹣2（x﹣2）（x+1）的值，其中x=2017．22.
如图，在7×7的正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的顶点都在正方形网格的格点上．
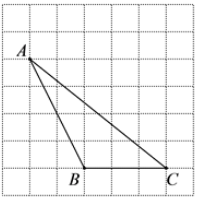
①画出△ABC的AC边上的中线BD．
②画出△ABC的BC边上的高线h．
③试在图中画出格点P，使得△PBC的面积与△ABC的面积相等，且△PBC为直角三角形．
23. 如图，BE是△ABC的角平分线，点D是AB边上一点，且∠DEB=∠DBE．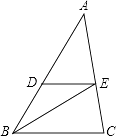
(1)、DE与BC平行吗？为什么？(2)、若∠A=40°，∠ADE=60°，求∠C的度数．24. 如图，在四边形ABCD中，∠A=∠C=90°，∠ABC，∠ADC的平分线分别与AD，BC相交于E，F两点，FG⊥BE于点G，∠1与∠2之间有怎样的数量关系？为什么？
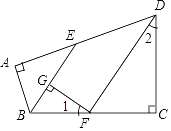25.教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：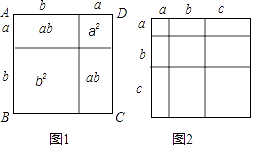
（i）把它看成是一个大正方形，则它的面积为（a+b）2；
（ii）把它看成是2个小长方形和2个小正方形组成的，则它的面积为a2+2ab+b2；因此，可得到等式：（a+b）2=a2+2ab+b2 ．
(1)、类比教材中的方法，由图2中的大正方形可得等式： ．(2)、试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图（标注好a，b） ，由图形可知，多项式2a2+3ab+b2可分解因式为： ．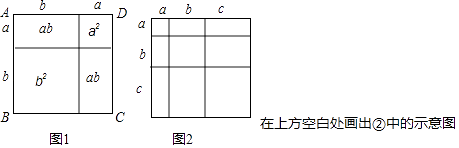
(3)、若将代数式（a1+a2+a3+…+a20）2展开后合并同类项，得到多项式N，则多项式N的项数一共有项．26. 如图1，直线AB∥CD，直线l与直线AB，CD相交于点E，F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处．
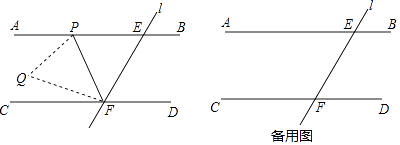(1)、若∠PEF=48°，点F恰好落在其中的一条平行线上，请直接写出∠EFP的度数．(2)、若∠PEF=75°，∠CFQ= ∠PFC，求∠EFP的度数．