2016-2017学年湖北省宜昌市枝江市九校联考七年级下学期期中数学试卷

试卷更新日期：2017-07-07 类型：期中考试

进入出卷网下载

一、选择题

1. 在实数﹣ $\frac{1}{3}$ ， $\sqrt{8}$ ， $\sqrt[3]{8}$ ，﹣0.518， $\frac{π}{3}$ ，| $\sqrt[3]{- 7}$ |， $\sqrt{2}$ 中，无理数的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 计算 $\sqrt{4}$ 的结果是（）

A、2 B、±2 C、﹣2 D、4

查看试题解析
3. 在同一个平面内，两条直线的位置关系是（　　）

A、平行或垂直 B、相交或垂直 C、平行或相交 D、不能确定

查看试题解析
4. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）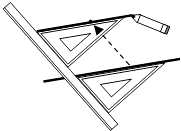

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、两直线平行，同位角相等

查看试题解析
5. 如图，直线a、b被直线c所截，若a∥b，∠1=130°，则∠2等于（）

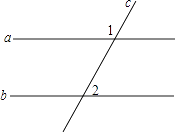A、30° B、40° C、50° D、60°

查看试题解析
6. 点P（﹣2，3）所在象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 下列从左到右的变形中，正确的是（）

A、 $\sqrt{81}$ =±9 B、﹣ $\sqrt{3.6}$ =﹣0.6 C、 $\sqrt{{(- 10)}^{2}}$ =﹣10 D、 $\sqrt[3]{- 5}$ =﹣ $\sqrt[3]{5}$

查看试题解析
8. 估计 $\sqrt{30}$ 的值（）

A、在3到4之间 B、在4到5之间 C、在5到6之间 D、在6到7之间

查看试题解析
9. 以下方程中，是二元一次方程的是（　　）

A、8x﹣y=y B、xy=3 C、3x+2y=3z D、y= $\frac{1}{x}$

查看试题解析
10. 方程组 ${\begin{matrix} 2 x + y = △ \\ x + y = 3 \end{matrix}$ 的解为 ${\begin{matrix} x = 1 \\ y = □ \end{matrix}$ ，则“△”、“□”代表的两个数分别为（）

A、5，2 B、1，3 C、4，2 D、2，3

查看试题解析
11. 若 $\sqrt[3]{0.367}$ =0.716， $\sqrt[3]{3.67}$ =1.542，则 $\sqrt[3]{367}$ =（）

A、15.42 B、7.16 C、154.2 D、71.6

查看试题解析
12. 把点（2，﹣3）先向右平移3个单位长度，再向上平移2个单位长度得到的点的坐标是（）

A、（5，﹣1） B、（﹣1，﹣5） C、（5，﹣5） D、（﹣1，﹣1）

查看试题解析
13. 若点P是第三象限内的点，且点P到x轴的距离是4，到y轴的距离是3，则点P的坐标是（）

A、（﹣4，﹣3） B、（4，﹣3） C、（﹣3，﹣4） D、（3，﹣4）

查看试题解析
14. 二元一次方程3a+b=9在正整数范围内的解的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析
15. 为保护生态环境，陕西省某县响应国家“退耕还林”号召，将某一部分耕地改为林地，改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各多少平方千米．设改变后耕地面积x平方千米，林地地面积y平方千米，根据题意，列出如下四个方程组，其中正确的是（）

A、 ${\begin{matrix} x + y = 180 \\ y = x \cdot 25 % \end{matrix}$ B、 ${\begin{matrix} x + y = 180 \\ x = y \cdot 25 % \end{matrix}$ C、 ${\begin{matrix} x + y = 180 \\ x - y = 25 % \end{matrix}$ D、 ${\begin{matrix} x + y = 180 \\ y - x = 25 % \end{matrix}$

查看试题解析

二、解答题

16. 计算 $\sqrt[3]{8} + \sqrt{{(- 5)}^{2}}$ ﹣ $| \sqrt{3} - 2 |$ ．

查看试题解析
17. 解方程组 ${\begin{matrix} x + 2 y = 9 \\ 3 x - 2 y = - 1 \end{matrix}$ ．

查看试题解析
18. 如图所示，已知BE平分∠ABC，∠1=∠2，求证：∠AED=∠C．完善以下推理过程．
证明：∵BE平分∠ABC，∴∠1=∠3．（）
又∵∠1=∠2（已知），∴ =（等量代换），
∴∥（）
∴∠AED=∠C （）．

查看试题解析
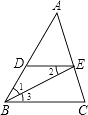19. 如图，已知∠1=∠2，∠B=∠C，试证明AB∥CD．

查看试题解析
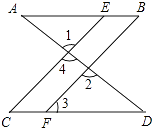20. 李欣同学昨天在文具店买了2本笔记本和4支多用笔，共花了14元；王凯以同样的价格买了2本笔记本和3支多用笔，共花了12元；问笔记本和多用笔的单价各是多少元？

查看试题解析
21. 在平面直角坐标系中，A、B、C三点的坐标分别为：A（﹣5，5）、B（﹣3，0）、C（0，3）．

(1)、①画出△ABC，它的面积为多少；
②在△ABC中，点A经过平移后的对应点A′（1，6），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出B′、C′的坐标；

(2)、
点P（﹣3，m）为△ABC内一点，将点P向右平移4个单位后，再向下平移6个单位得到点Q（n，﹣3），则m= ， n= ．

查看试题解析
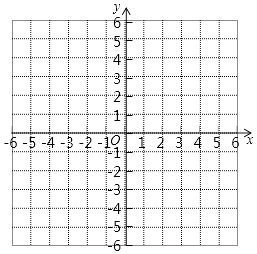22. 西北某地区为改造沙漠，决定从2012年起进行“治沙种草”，把沙漠地变为草地，并出台了一项激励措施：在“治沙种草”的过程中，每一年新增草地面积达到10亩的农户，当年都可得到生活补贴费1500元，且每超出一亩，政府还给予每亩a元的奖励．另外，经治沙种草后的土地从下一年起，平均每亩每年可有b元的种草收入．下表是某农户在头两年通过“治沙种草”每年获得的总收入情况：
（注：年总收入=生活补贴费+政府奖励费+种草收入）
年份
新增草地的亩数
年总收入
2012年
20亩
2600元
2013年
26亩
5060元

(1)、试根据提供的资料确定a、b的值；

(2)、观察数据，2013的新增草地的亩数在2012年新增草地的亩数上增加了一个百分数，若从2013年起，该农户每年新增草地的亩数均能比前一年按这个百分数增长，那么2015年该农户通过“治沙种草”获得的年总收入将达到多少元？

查看试题解析
23. 如图长方形OABC的位置如图所示，点B的坐标为（8，4），点P从点C出发向点O移动，速度为每秒1个单位；点Q同时从点O出发向点A移动，速度为每秒2个单位，设运动时间为t（0≤t≤4）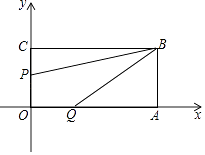

(1)、填空：点A的坐标为，点C的坐标为，点P的坐标为．（用含t的代数式表示）

(2)、当t为何值时，P、Q两点与原点距离相等？

(3)、在点P、Q移动过程中，四边形OPBQ的面积是否变化？说明理由．

查看试题解析
24.
已知，点E、F分别在直线AB，CD上，点P在AB、CD之间，连结EP、FP，如图1，过FP上的点G作GH∥EP，交CD于点H，且∠1=∠2．

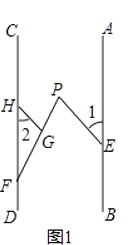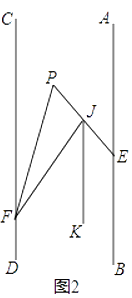
(1)、求证：AB∥CD；

(2)、
如图2，将射线FC沿FP折叠，交PE于点J，若JK平分∠EJF，且JK∥AB，则∠BEP与∠EPF之间有何数量关系，并证明你的结论；

(3)、
如图3，将射线FC沿FP折叠，将射线EA沿EP折叠，折叠后的两射线交于点M，当EM⊥FM时，求∠EPF的度数．

查看试题解析

年份	新增草地的亩数	年总收入
2012年	20亩	2600元
2013年	26亩	5060元