2016-2017学年广西贵港市平南县七年级下学期期中数学试卷

试卷更新日期：2017-07-07 类型：期中考试

进入出卷网下载

一、选择题

1. 方程x﹣2y=3，﹣6xy﹣5=0，x﹣ $\frac{1}{y}$ =4，3x﹣5z=4y，x²+y=1中是二元一次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列运算正确的是（）

A、a²•a³=a⁶ B、（﹣a³）²=﹣a⁶ C、（﹣3a²）²=6a⁴ D、（﹣a+b）（a+b）=b²﹣a²

查看试题解析
3. 下列各式由左边到右边的变形中，属于因式分解的是（）

A、x²﹣2x+2=x（x﹣2）+2 B、（x+y）（x﹣y）=x²﹣y² C、（2a﹣b）²=4a²﹣4ab+b² D、x²+4x+4=（x+2）²

查看试题解析
4. 用加减法解方程组 ${\begin{matrix} 2 x + 3 y = 3 \\ 3 x - 2 y = 11 \end{matrix}$ 时，下列四种变形中正确的是（）

A、 ${\begin{matrix} 4 x + 6 y = 3 \\ 9 x - 6 y = 11 \end{matrix}$ B、 ${\begin{matrix} 6 x + 3 y = 9 \\ 6 x - 2 y = 22 \end{matrix}$ C、 ${\begin{matrix} 4 x + 6 y = 6 \\ 9 x - 6 y = 33 \end{matrix}$ D、 ${\begin{matrix} 6 x + 9 y = 3 \\ 6 x - 4 y = 11 \end{matrix}$

查看试题解析
5. 因式分解与整数乘法一样，都是一种恒等变形，即在变形的过程中，形变值不变，于是将多项式x²﹣y²+（2x+2y）分解因式的结果为（）

A、（x+y）（x﹣y+2） B、（x+y）（x﹣y﹣2） C、（x﹣y）（x﹣y+2） D、（x﹣y）（x﹣y﹣2）

查看试题解析
6. 把多项式x²+ax+b分解因式，得（x+1）（x﹣3），则a，b的值分别是（）

A、a=﹣2，b=﹣3 B、a=2，b=3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
7. 计算（x﹣1）（2x+1）﹣（x²+x﹣2）的结果，与下列哪一个式子相同（）

A、x²﹣2x﹣3 B、x²﹣2x+1 C、x²+x﹣3 D、x²﹣3

查看试题解析
8. 已知x≠0且M=（x²+2x+1）（x²﹣2x+1），N=（x²+x+1）（x²﹣x+1），则M与N的大小关系为（）

A、M＞N B、M=N C、M＜N D、无法确定

查看试题解析
9. 利用图形中面积的等量关系可以得到某些数学公式．例如，根据图甲，我们可以得到两数和的平方公式：（a+b）²=a²+2ab+b² ．你根据图乙能得到的数学公式是（）

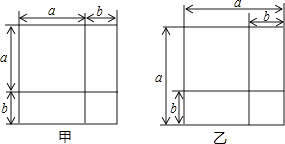A、（a+b）（a﹣b）=a²﹣b² B、（a﹣b）²=a²﹣2ab+b² C、a（a+b）=a²+ab D、a（a﹣b）=a²﹣ab

查看试题解析
10. 林林的妈妈给他买了一件上衣和一条裤子，共用去180元，其中上衣按标价打九折，裤子按标价打八五折，若上衣和裤子按标价算共计250元，求上衣和裤子的标价分别为多少元？设上衣标价为x元，裤子标价为y元，则可列出方程组为（）

A、 ${\begin{matrix} x + y = 180 \\ 0.9 x + 0.85 y = 250 \end{matrix}$ B、 ${\begin{matrix} x + y = 250 \\ 0.85 x + 0.9 y = 180 \end{matrix}$ C、 ${\begin{matrix} x + y = 250 \\ 0.9 x + 0.85 y = 180 \end{matrix}$ D、 ${\begin{matrix} x + y = 180 \\ 0.85 x + 0.9 y = 250 \end{matrix}$

查看试题解析
11. 2³²﹣1可以被10和20之间某两个整数整除，则这两个数是（）

A、17，15 B、17，16 C、15，16 D、13，14

查看试题解析
12. 关于x，y的二元一次方程组 ${\begin{matrix} x + y = 1 - m \\ x - 3 y = 5 + 3 m \end{matrix}$ 中，m与方程组的解中的x或y相等，则m的值为（）

A、3或 $\frac{1}{3}$ B、2或﹣ $\frac{1}{3}$ C、3或 $\frac{1}{2}$ D、2或﹣ $\frac{1}{2}$

查看试题解析

二、填空题

13. 化简3x²•（﹣2x）的结果．

查看试题解析
14. 把多项式x²+xy因式分解的结果是．

查看试题解析
15. 关于x，y定义运算：x*y=ax+by，若1*2=0，（﹣3）*3=﹣3，则a+b= ．

查看试题解析
16. 若|x+y﹣3|与（3xy﹣12）²互为相反数，则3x²+3y²的值为．

查看试题解析
17. 若多项式x²+2（m﹣2）x+25能用完全平方公式因式分解，则m的值为．

查看试题解析
18. 观察下列各式及展开式：
（a+b）²=a²+2ab+b²
（a+b）³=a³+3a²b+3ab²+b³
（a+b）⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
…
请你猜想（a+b）¹²的展开式第三项的系数是．

查看试题解析

三、解答题

19. 计算题

(1)、计算：993×1007

(2)、分解因式：﹣2a³+8a²﹣8a．

查看试题解析
20. 解下列方程组

(1)、 ${\begin{matrix} y - 2 x = 1 \\ 3 y + 2 x = 19 \end{matrix}$

(2)、 ${\begin{matrix} \frac{x}{2} - \frac{y}{3} = 1 \\ 3 x - 5 y = 3 \end{matrix}$ ．

查看试题解析
21. 已知x+y=4，x﹣y=2，求下列各式的值．

(1)、x²+y²

(2)、xy．

查看试题解析
22. 先化简，再求值（3x+2）（3x﹣2）﹣9x（x﹣1）+（x﹣2）² ，其中x=﹣3．

查看试题解析
23. 已知a²+8a+b²﹣2b+17=0，把多项式x²+4y²﹣axy﹣b因式分解．

查看试题解析
24. 在解决关于x，y的二元一次方程组 ${\begin{matrix} a x + b y = 3 \\ c x - 3 y = 5 \end{matrix}$ 时，小明由于粗心，把c写错解得 ${\begin{matrix} x = - 1 \\ y = 1 \end{matrix}$ ，小红正确地解得 ${\begin{matrix} x = 4 \\ y = - 3 \end{matrix}$ ，求a²b﹣ab²﹣c的值．

查看试题解析
25. 某中学去年通过“废品回收”活动筹集资金用于资助贫困山区中、小学生共27名，其中资助一名中学生的学习费用需要x元，资助一名小学生的学习费用需要y元，各年级学生筹集资金的数额及用其恰好资助中、小学生人数的部分情况如下表：
年级
筹集资金数额
资助贫困中学
资助贫困小学生人数（名）
七年级
5000
2
5
八年级
6000
3
5
九年级
8000

(1)、求x，y的值；

(2)、九年级学生筹集的资金数解决了其余贫困中、小学生的学习费用，求出九年级学生资助的贫困中、小学生人数．

查看试题解析
26. 观察下列各式：
（x﹣1）（x+1）=x²﹣1
（x﹣1）（x²+x+1）=x³﹣1
（x﹣1）（x³+x²+x+1）=x⁴﹣1
…

(1)、根据以上规律，则（x﹣1）（x⁷+x⁶+x⁵+x⁴+x³+x²+x+1）= ．

(2)、你能否由此归纳出一般性规律：
（x﹣1）（xⁿ^﹣¹+xⁿ^﹣²+…+x+1）= ．

(3)、根据上述的规律，求1+2+2²+…+2³⁸+2³⁹的值．

查看试题解析

年级	筹集资金数额	资助贫困中学	资助贫困小学生人数（名）
七年级	5000	2	5
八年级	6000	3	5
九年级	8000