广东省梅州市2019-2020学年9月高三上学期理数第一次质量检测试卷

试卷更新日期：2019-10-24 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x - 1 < 0}$ ， $B= {x | x^{2} = 2 x < 0}$ ，则 $A \cap B =$ （）

A、 ${x | x < 0}$ B、 ${x | x < 1}$ C、 ${x | 0 < x < 1}$ D、 ${x | 1 < x < 2}$

查看试题解析
2. 已知 $p$ ， $q \in R$ ， $1 + i$ 是关于 $x$ 的方程 $x^{2} + p x + q = 0$ 的一个根，则 $p \cdot q =$ （）

A、 $- 4$ B、 $0$ C、 $2$ D、 $4$

查看试题解析
3. 已知 $a = \ln 3$ ， $b = \log_{3} 10$ ， $c = \lg 3$ ，则 $a$ ， $b$ ， $c$ 的大小关系为（）

A、 $c < b < a$ B、 $a < c < b$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析
4. 函数 $f (x) = \frac{x^{2} - 1}{| x |}$ 的图象大致为（）

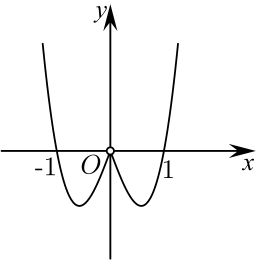
A、 B、 C、 D、

查看试题解析
5. 下图来自古希腊数学家希波克拉底所研究的几何图形，此图由一个半圆和一个四分之一圆构成，两个阴影部分分别标记为 $A$ 和 $M$ .在此图内任取一点，此点取自 $A$ 区域的概率记为 $P (A)$ ，取自 $M$ 区域的概率记为 $P (M)$ ，则（）

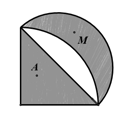A、 $P (A) > P (M)$ B、 $P (A) < P (M)$ C、 $P (A) = P (M)$ D、 $P (A)$ 与 $P (M)$ 的大小关系与半径长度有关

查看试题解析
6. 下图是判断输入的年份 $x$ 是否是闰年的程序框图，若先后输入 $x = 1900$ ， $x = 2400$ ，则输出的结果分别是（注： $x M O D y$ 表示 $x$ 除以 $y$ 的余数）（）

A、 $1900$ 是闰年， $2400$ 是闰年 B、 $1900$ 是闰年， $2400$ 是平年 C、 $1900$ 是平年， $2400$ 是闰年 D、 $1900$ 是平年， $2400$ 是平年

查看试题解析
7. 若 $\sin 78^{\circ} = m$ ，则 $\sin 6^{\circ} =$ （）

A、 $\sqrt{\frac{m + 1}{2}}$ B、 $\sqrt{\frac{1 - m}{2}}$ C、 $\frac{\sqrt{m + 1}}{2}$ D、 $\frac{\sqrt{1 - m}}{2}$

查看试题解析
8. 已知等差数列 ${a_{n}}$ 的公差不为零，其前 $n$ 项和为 $S_{n}$ ，若 $S_{3}$ ， $S_{9}$ ， $S_{27}$ 成等比数列，则 $\frac{S_{9}}{S_{3}} =$ （）

A、 $3$ B、 $6$ C、 $9$ D、 $12$

查看试题解析
9. 双曲线 $C ： \frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的右焦点为 $F$ ，点 $P$ 为 $C$ 的一条渐近线上的点， $O$ 为坐标原点，若 $| P O | = | P F |$ ，则 $S_{Δ O P F}$ 的最小值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $1$ D、 $2$

查看试题解析
10. 已知函数 $f (x) = \ln \frac{x}{4 - x}$ ，则（）

A、 $y = f (x)$ 的图象关于点 $(2 ， 0)$ 对称 B、 $y = f (x)$ 的图象关于直线 $x = 2$ 对称 C、 $f (x)$ 在 $(0 ， 4)$ 上单调递减 D、 $f (x)$ 在 $(0 ， 2)$ 上单调递减，在 $(2 ， 4)$ 上单调递增

查看试题解析
11. 已知函数 $f (x) = a \sin x - \sqrt{3} \cos x$ 的图像的一条对称轴为直线 $x = \frac{5 π}{6}$ ，且 $f (x_{1}) \cdot f (x_{2}) = - 4$ ，则 $| x_{1} + x_{2} |$ 的最小值为（）

A、 $- \frac{π}{3}$ B、0 C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
12. 设 $f (x)$ 是定义在 $R$ 上的偶函数， $\forall x \in R$ ，都有 $f (2 - x) = f (2 + x)$ ，且当 $x \in [0 ， 2]$ 时， $f (x) = 2^{x} - 2$ ，若函数 $g (x) = f (x) - \log_{a} (x + 1)$ （ $a > 0$ ， $a \neq 1$ ）在区间 $(- 1 ， 9]$ 内恰有三个不同零点，则实数 $a$ 的取值范围是（）

A、 $(0 ， \frac{1}{9}) \cup (\sqrt{7} ， + \infty)$ B、 $(\frac{1}{9} ， 1) \cup (1 ， \sqrt{3})$ C、 $(\frac{1}{9} ， \frac{1}{5}) \cup (\sqrt{3} ， \sqrt{7})$ D、 $(\frac{1}{7} ， \frac{1}{3}) \cup (\sqrt{5} ， 3)$

查看试题解析

二、填空题

13. 若 $x ， y$ 满足约束条件 ${\begin{array}{l} x - y + 2 \geq 0 \\ 2 x - y + 1 \leq 0 \\ x - 2 y + 2 \leq 0 \end{array}$ ，则 $z = 3 x - y$ 的最大值为.

查看试题解析
14. 已知 $\vec{e_{1}} ， \vec{e_{2}}$ 是夹角为 $60 °$ 的两个单位向量， $\vec{a} = \vec{e_{1}} - \vec{e_{2}} ， \vec{b} = \vec{e_{1}} - 2 \vec{e_{2}}$ ，则 $\vec{a} \cdot \vec{b} =$ .

查看试题解析
15. 已知函数 $f (x) = \sin (ω x + \frac{π}{4}) (ω > 0)$ ，若 $f (x)$ 在 $[0 ， 2 π]$ 上恰有 $3$ 个极值点，则 $ω$ 的取值范围是.

查看试题解析
16. 在三棱锥 $P - A B C$ 中， $∠ B A C = 60 °$ ， $∠ P B A = ∠ P C A = 90 °$ ， $P B = P C = \sqrt{3}$ ，点 $P$ 到底面 $A B C$ 的距离为 $\sqrt{2}$ ，则三棱锥 $P - A B C$ 的外接球的表面积为.

查看试题解析

三、解答题

17. $△ A B C$ 的内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，已知 $△ A B C$ 的面积为 $S = \frac{1}{6} b^{2} \tan A$ .

(1)、证明： $b = 3 c \cos A$ ；

(2)、若 $\tan A = 2 ， a = 2 \sqrt{2} ，$ 求 $S$ .

查看试题解析
18. 某音乐院校举行“校园之星”评选活动，评委由本校全体学生组成，对 $A ， B$ 两位选手，随机调查了 $20$ 个学生的评分，得到下面的茎叶图：

(1)、通过茎叶图比较 $A ， B$ 两位选手所得分数的平均值及分散程度（不要求计算出具体值，得出结论即可）；

(2)、校方将会根据评分记过对参赛选手进行三向分流：

所得分数

低于 $60$ 分

$60$ 分到 $79$ 分

不低于 $80$ 分

分流方向

淘汰出局

复赛待选

直接晋级

记事件 $C$ “ $A$ 获得的分流等级高于 $B$ ”，根据所给数据，以事件发生的频率作为相应事件发生的概率，求事件 $C$ 发生的概率.

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是矩形，侧棱 $P D ⊥$ 底面 $A B C D$ ， $P D = D C$ ，点 $E$ 是 $P C$ 的中点.

(1)、求证： $P A / /$ 平面 $B D E$ ；

(2)、若直线 $B D$ 与平面 $P B C$ 所成角为 $30 °$ ，求二面角 $C - P B - D$ 的大小.

查看试题解析
20. 已知 $F$ 为抛物线 $T ： x^{2} = 4 y$ 的焦点，直线 $l ： y = k x + 2$ 与 $T$ 相交于 $A ， B$ 两点.

(1)、若 $k = 1$ ，求 $| F A | + | F B |$ 的值；

(2)、点 $C (- 3 ， - 2)$ ，若 $∠ C F A = ∠ C F B$ ，求直线 $l$ 的方程.

查看试题解析
21. 已知函数 $f (x) = x \sin x$ ， $x \in (0 ， π)$ ， $f^{'} (x)$ 为 $f (x)$ 的导数，且 $g (x) = f^{'} (x)$ .证明：

(1)、 $g (x)$ 在 $(2 ， \frac{2 π}{3})$ 内有唯一零点；

(2)、 $f (x) < 2$ .
（参考数据： $\sin 2 \approx 0.9903$ ， $\cos 2 \approx - 0.4161$ ， $\tan 2 \approx - 2.1850$ ， $\sqrt{2} \approx 1.4142$ ， $π \approx 3.14$ .）

查看试题解析
22. 在极坐标系中，圆ρ=4cosθ .以极点 $O$ 为原点，极轴为 $x$ 轴正半轴建立直角坐标系 $x O y$ ，直线 $l$ 经过点 $M (- 1 ， - 3 \sqrt{3})$ 且倾斜角为 $α$ .

(1)、求圆 $C$ 的直角坐标方程和直线 $l$ 的参数方程；

(2)、已知直线 $l$ 与圆 $C$ 交与 $A$ ， $B$ ，满足 $A$ 为 $M B$ 的中点，求 $α$ .

查看试题解析
23. 设函数 $f (x) = | 2 x - 1 | + | x + 1 |$ .

(1)、画出 $y = f (x)$ 的图像；

(2)、若 $f (x) \leq m | x | + n$ ，求 $m + n$ 的最小值.

查看试题解析

所得分数	低于 $60$ 分	$60$ 分到 $79$ 分	不低于 $80$ 分
分流方向	淘汰出局	复赛待选	直接晋级