初中数学华师大版九年级上学期 第24章 24.4 解直角三角形
试卷更新日期:2019-10-23 类型:同步测试
一、单选题
-
1. 某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
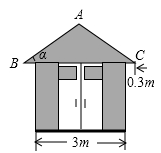 A、 米 B、 米 C、 米 D、 米2. 小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处.看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7.sin65°≈0.9.cos65°≈0.4,tan65°≈2.1)( )
A、 米 B、 米 C、 米 D、 米2. 小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处.看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7.sin65°≈0.9.cos65°≈0.4,tan65°≈2.1)( )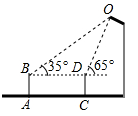 A、3.2米 B、3.9米 C、4.7米 D、5.4米3. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A、3.2米 B、3.9米 C、4.7米 D、5.4米3. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )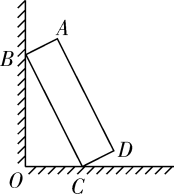 A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx4. 如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )
A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx4. 如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )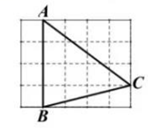 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 如图,在△ABC中,若∠A=45°,AC2-BC2= AB2 , 则tanC=。
 6. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 .
6. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 . 7. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.
7. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.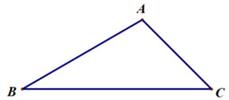
三、解答题
-
8. 如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.求A,B间的距离.( ≈1.73, ≈1.4,结果保留一位小数).
 9. 图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
9. 图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)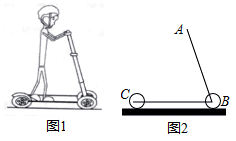 10. 如图,两座建筑物的水平距离BC为40m,从A点测得D点的俯角α为45°,测得C点的俯角β为60°。求这两座建筑物AB,CD的高度。(结果保留小数点后一位 )
10. 如图,两座建筑物的水平距离BC为40m,从A点测得D点的俯角α为45°,测得C点的俯角β为60°。求这两座建筑物AB,CD的高度。(结果保留小数点后一位 )
四、综合题
-
11. 如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上。
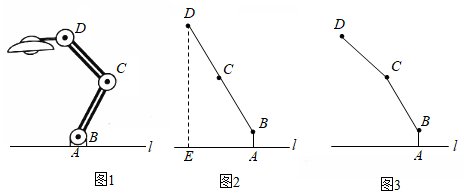 (1)、转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.(2)、将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据: ≈1.41, ≈1.73)12. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行.
(1)、转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.(2)、将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据: ≈1.41, ≈1.73)12. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行. (1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米, ≈1.41, ≈1.73).
(1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米, ≈1.41, ≈1.73).