初中数学华师大版九年级上学期 第23章测试卷
试卷更新日期:2019-10-23 类型:单元试卷
一、单选题
-
1. 在平面直角坐标系中,将点 向上平移3个单位长度,再向左平移2个单位长度,得到点 ,则点 的坐标是( ).A、 B、 C、 D、2. 以原点O为位似中心,作△ABC的位似图形△A'B'C',△ABC与△A'B'C'相似比为3,若点C的坐标为(4,1),则点C’的坐标为( )A、(12,3) B、(﹣12,3)或(12,﹣3) C、(﹣12,﹣3) D、(12,3)或(﹣12,﹣3)3. 如图,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1 , S2 , 则下列结论错误的是( )
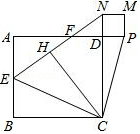 A、S1+S2=CP2 B、AF=2FD C、CD=4PD D、cos∠HCD=4. 如图,矩形 中, 与 相交于点 , ,将 沿 折叠,点 的对应点为 ,连接 交 于点 ,且 ,在 边上有一点 ,使得 的值最小,此时 ( )
A、S1+S2=CP2 B、AF=2FD C、CD=4PD D、cos∠HCD=4. 如图,矩形 中, 与 相交于点 , ,将 沿 折叠,点 的对应点为 ,连接 交 于点 ,且 ,在 边上有一点 ,使得 的值最小,此时 ( )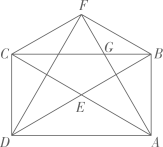 A、 B、 C、 D、5. 如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于( )
A、 B、 C、 D、5. 如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于( )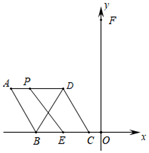 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为.
 7. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.8. 如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm.
7. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.8. 如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm. 9. 如图,原点O是△ABC和△A’B’C’的位似中心,点A(1,0)与点A’(-2,0)是对应点,△ABC的面积是 ,则△A’B’C’的面积是
9. 如图,原点O是△ABC和△A’B’C’的位似中心,点A(1,0)与点A’(-2,0)是对应点,△ABC的面积是 ,则△A’B’C’的面积是 10. 如图,在平面直角坐标系中, 的直角顶点 的坐标为 ,点 在 轴正半轴上,且 .将 先绕点 逆时针旋转 ,再向左平移3个单位,则变换后点 的对应点的坐标为.
10. 如图,在平面直角坐标系中, 的直角顶点 的坐标为 ,点 在 轴正半轴上,且 .将 先绕点 逆时针旋转 ,再向左平移3个单位,则变换后点 的对应点的坐标为.
三、解答题
-
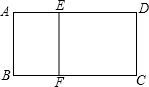
11. 如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
四、综合题
-
12. 如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)、以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2(2)、连接⑴中的AA′,求四边形AA′C′C的周长.(结果保留根号)13. 在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B. (1)、k的值是;(2)、点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
(1)、k的值是;(2)、点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求▱OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 ,请直接写出点C的坐标.
14. 如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.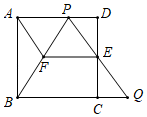 (1)、求证: ;(2)、过点E作 交PB于点F,连结AF,当 时,①求证:四边形AFEP是平行四边形;
(1)、求证: ;(2)、过点E作 交PB于点F,连结AF,当 时,①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.
-