初中数学华师大版九年级上学期 第23章 23.4 中位线
试卷更新日期:2019-10-23 类型:同步测试
一、单选题
-
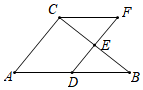
1. 如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
 A、 B、 C、 D、2. 如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
A、 B、 C、 D、2. 如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( ) A、DE是△BCD的中线 B、BD是△ABC的中线 C、AD=DC,BE=EC D、AD=EC,DC=BE3. 给出以下判断:
A、DE是△BCD的中线 B、BD是△ABC的中线 C、AD=DC,BE=EC D、AD=EC,DC=BE3. 给出以下判断:
(1)线段的中点是线段的重心
(2)三角形的三条中线交于一点,这一点就是三角形的重心
(3)平行四边形的重心是它的两条对角线的交点
(4)三角形的重心是它的中线的一个三等分点
那么以上判断中正确的有( )A、一个 B、两个 C、三个 D、四个二、填空题
-
4. 如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选适当的点C,连结AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22m,则AB=m.
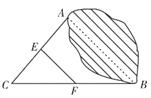 5. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=.
5. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=. 6. 如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,若AD=BC= ,则四边形EGFH的周长是.
6. 如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,若AD=BC= ,则四边形EGFH的周长是. 7. 如图,在 中, , , 为 的中位线,延长 至 ,使 ,连接 并延长交 于点 .若 ,则 的周长为 .
7. 如图,在 中, , , 为 的中位线,延长 至 ,使 ,连接 并延长交 于点 .若 ,则 的周长为 .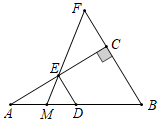 8. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 .
8. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 .
三、作图题

