2017年广东省广州市海珠区中考数学一模试卷

试卷更新日期：2017-07-07 类型：中考模拟

进入出卷网下载

一、选择题

1. 如果向东走50m记为50m，那么向西走30m记为（）

A、﹣30m B、|﹣30|m C、﹣（﹣30）m D、 $\frac{1}{30}$ m

查看试题解析
2. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图，点A．B．C在⊙D上，∠ABC=70°，则∠ADC的度数为（）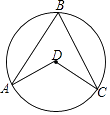

A、110° B、140° C、35° D、130°

查看试题解析
4. 如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是（）

A、3x²•4x²=12x² B、 $\frac{x^{2}}{y^{2}} = \frac{x}{y}$ （y≠0） C、2 $\sqrt{x} + 3 \sqrt{y} = 5 \sqrt{x y}$ （x≥0，y≥0） D、xy²÷ $\frac{1}{2 y} = 2 x y^{3}$ （y≠0）

查看试题解析
6. 下列命题中，假命题是（）

A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、对角线相等的平行四边形是矩形

查看试题解析
7. 下列函数中，y随x的增大而增大的是（）

A、y= $\frac{3}{x}$ B、y=﹣x+5 C、y= $\frac{1}{2}$ x D、y= $\frac{1}{2} x^{2}$ （x＜0）

查看试题解析
8. 如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD．若BD=1，则AC的长是（）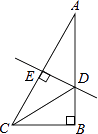

A、2 $\sqrt{3}$ B、2 C、4 $\sqrt{3}$ D、4

查看试题解析
9. 已知抛物线y=ax²+bx+c的图象如图所示，顶点为（4，6），则下列说法错误的是（）

A、b²＞4ac B、ax²+bx+c≤6 C、若点（2，m）（5，n）在抛物线上，则m＞n D、8a+b=0

查看试题解析
10.
如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为 $(\sqrt{2} ， \sqrt{2})$ ，点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

11. 在不透明口袋内有形状．大小．质地完全一样的5个小球，其中红球3个，白球2个，随机抽取一个小球是红球的概率是．

查看试题解析
12. 分解因式：3x²﹣6xy= ．

查看试题解析
13. 某饮料店为了解本店一种罐装饮料上半年的销售情况，随机调查了6天该种饮料的日销售情况，结果如下（单位：罐）：33，28，32，25，24，30，这6天销售量的中位数是．

查看试题解析
14. 某公司制作毕业纪念册的收费如下：设计费与加工费共1000元，另外每册收取材料费4元，则总收费y与制作纪念册的册数x的函数关系式为．

查看试题解析
15. 如图，AB是⊙O的直径，AC．BC是⊙O的弦，直径DE⊥BC于点M．若点E在优弧 $\hat{C A B}$ 上，AC=8，BC=6，则EM= ．

查看试题解析
16. 若一元二次方程ax²+bx+1=0有两个相同的实数根，则a²﹣b²+5的最小值为．

查看试题解析

三、解答题

17. 综合题。

(1)、解不等式组 ${\begin{matrix} x - 1 < 0 \\ 8 + 3 (x - 1) \geq - 4 \end{matrix}$

(2)、解方程 $\frac{2}{x - 3} = \frac{1}{x + 1}$ ．

查看试题解析
18. 如图，AC是菱形ABCD的对角线，点E、F分别在边AB、AD上，且AE=AF．
求证：△ACE≌△ACF．

查看试题解析
19. 已知A=（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 2}{x^{2} - 4 x + 4}$ ）• $\frac{x^{2} - 4}{x + 2}$

(1)、化简A；

(2)、若x满足x²﹣2x﹣8=0，求A的值．

查看试题解析
20. 中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注．某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度，对该校九年级部分学生进行了随机抽样调查，并绘制出如图所示的两幅统计图．在条形图中，从左向右依次为：A 级（非常喜欢），B 级（较喜欢），C 级（一般），D 级（不喜欢）．请结合两幅统计图，回答下列问题：

(1)、本次抽样调查的样本容量是，表示“D级（不喜欢）”的扇形的圆心角为°；

(2)、若该校九年级有200名学生．请你估计该年级观看“中国诗词大会”节目B 级（较喜欢）的学生人数；

(3)、若从本次调查中的A级（非常喜欢）的5名学生中，选出2名去参加广州市中学生诗词大会比赛，已知A级学生中男生有3名，请用“列表”或“画树状图”的方法求出所选出的2名学生中至少有1名女生的概率．

查看试题解析
21. 某小区为更好的提高业主垃圾分类的意识，管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买3个温馨提示牌和4个垃圾箱共需580元，且每个温馨提示牌比垃圾箱便宜40元．

(1)、问购买1个温馨提示牌和1个垃圾箱各需多少元？

(2)、如果需要购买温馨提示牌和垃圾箱共100个，费用不超过8000元，问最多购买垃圾箱多少个？

查看试题解析
22. 如图，在△ABC 中，∠C=90°

(1)、利用尺规作∠B 的角平分线交AC于D，以BD为直径作⊙O交AB于E（保留作图痕迹，不写作法）；

(2)、综合应用：在（1）的条件下，连接DE
①求证：CD=DE；
②若sinA= $\frac{3}{5}$ ，AC=6，求AD．

查看试题解析
23.
如图，在平面直角坐标系中，一次函数y₁=ax+b（a≠0）的图象与y轴相交于点A，与反比例函数y₂= $\frac{k}{x}$ （c≠0）的图象相交于点B（3，2）、C（﹣1，n）．

(1)、求一次函数和反比例函数的解析式；

(2)、根据图象，直接写出y₁＞y₂时x的取值范围；

(3)、在y轴上是否存在点P，使△PAB为直角三角形？如果存在，请求点P的坐标；若不存在，请说明理由．

查看试题解析
24. 抛物线y=ax²+c与x轴交于A、B两点（A在B的左边），与y轴交于点C，抛物线上有一动点P

(1)、若A（﹣2，0），C（0，﹣4）
①求抛物线的解析式；
②在①的情况下，若点P在第四象限运动，点D（0，﹣2），以BD、BP为邻边作平行四边形BDQP，求平行四边形BDQP面积的取值范围．

(2)、若点P在第一象限运动，且a＜0，连接AP、BP分别交y轴于点E、F，则问 $\frac{S_{△ A O E} + S_{△ B O F}}{S_{△ A B C}}$ 是否与a，c有关？若有关，用a，c表示该比值；若无关，求出该比值．

查看试题解析
25. 如图：AD与⊙O相切于点D，AF经过圆心与圆交于点E、F，连接DE、DF，且EF=6，AD=4．

(1)、证明：AD²=AE•AF；

(2)、延长AD到点B，使DB=AD，直径EF上有一动点C，连接CB交DF于点G，连接EG，设∠ACB=α，BG=x，EG=y．
①当α=90⁰时，探索EG与BD的大小关系？并说明理由；
②当α=120⁰时，求y与x的关系式，并用x的代数式表示y．

查看试题解析