初中数学北师大版九年级上学期 第四章测试卷
试卷更新日期:2019-10-21 类型:单元试卷
一、单选题
-
1. 若 ,相似比为 ,则 与 的周长的比为( )A、 B、 C、 D、2. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
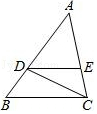 A、2 B、3 C、2 D、53. 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;② ;③AC BE=12;④3BF=4AC;其中正确结论的个数有( )
A、2 B、3 C、2 D、53. 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;② ;③AC BE=12;④3BF=4AC;其中正确结论的个数有( )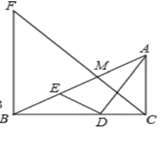 A、1个 B、2个 C、3个 D、4个4. 如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( )
A、1个 B、2个 C、3个 D、4个4. 如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( )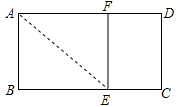 A、 B、
A、 B、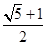 C、
D、2
5. 如下图,四边形ABCD和A’B’C’D’是以点O为位似中心的位似图形,若OA’:OA=3:5,四边形A’B’C’D’的面积为9 cm2 , 则四边形ABCD的面积为( )
C、
D、2
5. 如下图,四边形ABCD和A’B’C’D’是以点O为位似中心的位似图形,若OA’:OA=3:5,四边形A’B’C’D’的面积为9 cm2 , 则四边形ABCD的面积为( )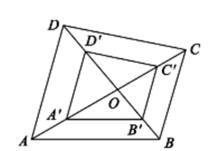 A、15cm2 B、25cm2 C、18cm2 D、27cm2
A、15cm2 B、25cm2 C、18cm2 D、27cm2二、填空题
-
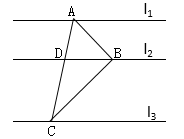
6. 若 = ,则 的值为.7. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.
 8. 如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为米.
8. 如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为米. 9. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,以AC为斜边作Rt△ACC1 , 使∠CAC1=30°,Rt△ACC1的面积记为S1 , 则S1=;再以AC1为斜边作Rt△AC1C2 , 使∠C1AC2=30°,Rt△AC1C2的面积记为S2 , ……,以此类推,则Sn=(用含n的式子表示)
9. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,以AC为斜边作Rt△ACC1 , 使∠CAC1=30°,Rt△ACC1的面积记为S1 , 则S1=;再以AC1为斜边作Rt△AC1C2 , 使∠C1AC2=30°,Rt△AC1C2的面积记为S2 , ……,以此类推,则Sn=(用含n的式子表示)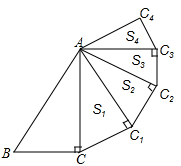
三、作图题
-
10. 如图,△ABC三个顶点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
 (1)、①将△ABC向右平移4个单位,请画出平移后的△A1B1C1;
(1)、①将△ABC向右平移4个单位,请画出平移后的△A1B1C1;②以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在网格内画出△A2B2C2;
(2)、请在x轴上找出点P,使得点P到B与点A1距离之和最小,请直接写出P点的坐标.四、综合题
-
11. 在矩形 中,连结 ,点E从点B出发,以每秒1个单位的速度沿着 的路径运动,运动时间为t(秒).过点E作 于点F , 在矩形 的内部作正方形 .
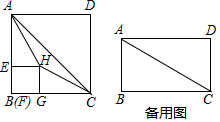 (1)、如图,当 时,
(1)、如图,当 时,①若点H在 的内部,连结 、 ,求证: ;
②当 时,设正方形 与 的重叠部分面积为S , 求S与t的函数关系式;
(2)、当 , 时,若直线 将矩形 的面积分成1︰3两部分,求t的值.
-

