云南省玉溪市易门县2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-21 类型：期中考试
一、单选题
-
1. 下列图形分别是四个城市电视台的台徽，其中为轴对称图形的是（ ）A、
B、
C、
D、
2. 对于任意三角形的高，下列说法不正确的是（ ）A、直角三角形只有一条高 B、锐角三角形有三条高 C、任意三角形都有三条高 D、钝角三角形有两条高在三角形的外部3. 一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（ ）A、5或7 B、7或9 C、7 D、94. 等腰三角形的一个角是80°，则它的底角是（）A、50° B、80° C、50°或80° D、20°或80°5. 现有四根木棒，长度分别为4，6，8，10，从中任取三根木棒，能组成三角形的个数为（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，△ABC中，AD⊥BC，D为BC的中点，以下结论：（1）△ABD≌△ACD；（2）AB=AC；（3）∠B=∠C；（4）AD是△ABC的角平分线．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个7. 用正三角形、正四边形和正六四边形按如图所示的规律拼图案，即从第二个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个.则第n个图案中正三角形的个数为（ ）(用含n的代数式表示).
A、2n＋1 B、3n＋2 C、4n＋2 D、4n－2二、填空题
-
8. 若A（x，3）关于y轴的对称点是B（－2，y），则x＝ ， y＝ ， 点A关于x轴的对称点的坐标是.9. 如图：ΔABE≌ΔACD，AB=10cm，∠A=60°，∠B=30°，则AD=cm，∠ADC=。
10. 如图，已知线段AB、CD相交于点O，且∠A＝∠B，只需补充一个条件 ， 则有△AOC≌△BOD.
11. 如图，直线a、b、c表示三条公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有处。
12. 如图，七星形中∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G=.
13. 如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，这样一直走下去，他第一次回到出发点A时，一共走了m
14. 如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配.（ ）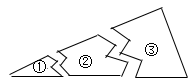
A、① B、② C、③ D、①和②三、解答题
-
15. 一个多边形的内角和比它外角和的3少180°，求这个多边形的边数.16. 如图，△ABC中，AB=AC=CD，BD=AD，求△ABC中各角的度数。
17. 如图，已知点B、E、C、F在同一直线上，AB=DE，∠A=∠D，AC∥DF.
求证：
(1)、△ABC≌△DEF；(2)、BE=CF18. 如图，AB⊥AC，CD⊥BD，AC、BD相交于点O.
①已知AB＝CD，利用可以判定△ABO≌△DCO；
②已知AB＝CD，∠BAD＝∠CDA，利用可以判定△ABD≌△DCA；
③已知AC＝BD，利用可以判定△ABC≌△DBC；
④已知AO＝DO，利用可以判定△ABO≌△DCO；
⑤已知AB＝CD，BD＝AC，利用可以判定△ABD≌△DCA；
19. △ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．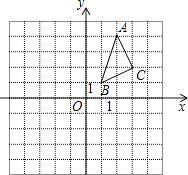
①作出△ABC关于x轴对称的△A1B1C1 ， 并写出点C1的坐标；
②作出△ABC关于y对称的△A2B2C2 ， 并写出点C2的坐标．
20. 完成下面的证明过程已知：如图，AB∥CD，AE⊥BD于E，CF⊥BD于F，BF＝DE.
求证：△ABE≌△CDF.
证明：∵AB∥CD，∴∠1＝.（两直线平行，内错角相等）
∵AE⊥BD，CF⊥BD，
∴∠AEB＝＝90°.
∵BF＝DE，∴BE＝.
在△ABE和△CDF中，
①；②；③；
∴△ABE≌△CDF.
21. 如图，AD为△ABC的中线，BE为△ABD的中线.
(1)、∠ABE＝15°，∠BAD＝40°，求∠BED的度数；(2)、若△ABC的面积为40，BD＝5，则E到BC边的距离为多少.
