湖北省武汉市青山区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-21 类型：期中考试
一、单选题
-
1. 下列博物院的标识中是轴对称图形的是（ ）A、
B、
C、
D、
2. 在△ABC中，AB=3cm，AC=5cm.若BC的长为整数，则BC的长可能是（ ）A、7cm B、8cm C、1cm D、2cm3. 在平面直角坐标中，点P(2，1)关于x轴对称点的坐标是（ ）A、(2，-1) B、(2，1) C、(-2，-1) D、(-2，1)4. 已知一个多边形的内角和是900°，则这个多边形是（ ）A、五边形 B、七边形 C、九边形 D、不能确定5. 如图，木工师傅做完窗框后，常像图中那样钉上一条斜拉的木条，这样做的数学原理是（ ）
A、全等三角形对应角相等 B、三角形内角和为180° C、三角形的稳定性 D、两直线平行，内错角相等6. 如图，∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是（ ）
A、∠C=∠D B、∠ABC=∠ABD C、AC=AD D、BC=BD7. 如图，将锐角△ABC沿DH、GF、FE翻折，三个顶点均落在点O处.若∠1=85°，则∠2的度数为（ ）
A、75° B、85° C、90° D、95°8. 在▱ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，则AB的长为（ ）A、3 B、5 C、3或5 D、2或39. 在△ABC中，边AC，BC的垂直平分线的交点O落在边AB上，则△ABC的形状是（ ）A、钝角三角形 B、直角三角形 C、锐角三角形 D、任意三角形10. 如图，在Rt△ABC中，∠ACB=90°，BC=5，点P在边AB上，连接CP.将△BCP沿直线CP翻折后，点B恰好落在边AC的中点处，则点P到AC的距离是（ ）
A、2.5 B、 C、3.5 D、二、填空题
-
11. 如图，∠A＝60°，∠ACD＝110°，∠B＝°.
12. 如图，△ABC≌△A’B’C’，AB=2，BC=4.2，CA=5.5，则C’A’=.
13. 如图，在△ABC中，AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交边AC于点E，则△BCE的周长为 ．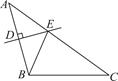
14. 一个正方形和两个等边三角形的位置如图所示，则∠1+∠2+∠3的度数为.
15. 如图，在3×3的正方形网络中，与△ABC关于某条直线对称的格点三角形（顶点在格线交点的三角形）共有个.
16. 如图，Rt△ABC中，AB=AC，∠BAC=90°，BE⊥CE，垂足是E，BE交AC于点D，F是BE上一点，AF⊥AE，且C是线段AF的垂直平分线上的点，AF=2 ，则DF=.
三、解答题
-
17. 如图，在△ABC中，∠C=65°，AD为BC边上的高.
(1)、求∠CAD的度数；(2)、若∠B=45°，AE平分∠BAC，求∠EAD的度数.18. 如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，AF与DE交于点G.求证：△ABF≌△DCE.
19. 已知等腰三角形△ABC的一边长为5，周长为22.求△ABC另两边的长.20. 如图，B、C、E三点在同一条直线上，AB∥DC，BC=DC，∠ACD=∠E.
求证：
(1)、∠ACB=∠D；(2)、AB=EC.21. 如图，在Rt△ABC中，∠A=30°，∠ACB=90°，点D为AC中点，点E为AB边上一动点，AE=DE，延长ED交BC的延长线于点F.
(1)、求证：△BEF是等边三角形；(2)、若AB=12，求DE的长.22. 在△ABC中，AB=AC，∠CAB=50°.在△ABC的外侧作直线AP，作点C关于直线AP的对称点D，连接BD，CD，AD，其中BD交直线AP于点E.
(1)、如图1，与AD相等的线段是；(2)、如图2，若∠PAC=20°，求∠BDC的度数；(3)、如图3，当65°<∠PAC<130°时，作AF⊥CE于点F，若EF=1，BE=5，求DE的长.23. 如图1，在五边形ABCDE中，∠E=90°，BC=DE.连接AC，AD，且AB=AD，AC⊥BC.
(1)、求证：AC=AE；(2)、如图2，若∠ABC=∠CAD，AF为BE边上的中线，求证：AF⊥CD；(3)、如图3，在（2）的条件下，AE=6，DE=4，则五边形ABCDE的面积为.24. 如图1，点A(2，1)，点A与点B关于y轴对称，AC∥y轴，且AC=3，连接BC交y轴于点D.
(1)、点B的坐标为 ， 点C的坐标为；(2)、如图2，连接OC，OC平分∠ACB，求证：OB⊥OC；(3)、如图3，在（2）的条件下，点P为OC上一点，且∠PAC=45°，求点P的坐标.