湖北省武汉市江汉区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-21 类型：期中考试
一、单选题
-
1. 有4cm和6cm的两根小棒，请你再找一根小棒，并以这三根小棒为边围成一个三角形，下列长度的小棒可选的是（ ）A、1cm B、2cm C、7cm D、10cm2. 如图，∠ABC＝∠ABD，还应补充一个条件，才能推出△ABC≌△ABD.补充下列其中一个条件后，不一定能推出△ABC≌△ABD的是（ ）
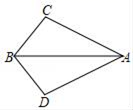A、BC＝BD B、AC＝AD C、∠ACB＝∠ADB D、∠CAB＝∠DAB3. 下列运算中，正确的是（ ）A、x+x＝x2 B、3x2﹣2x＝x C、（x2）3＝x6 D、x2•x3＝x64. 工人师傅经常利用角尺平分一个任意角，如图所示，∠AOB是一个任意角，在边OA，OB上分别取OD=OE，移动角尺，使角尺两边相同的刻度分别与D，E重合，这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是（ ）
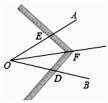A、SAS B、ASA C、AAS D、SSS5. 计算（﹣4a2+12a3b）÷（﹣4a2）的结果是（ ）A、1﹣3ab B、﹣3ab C、1+3ab D、﹣1﹣3ab6. 如图，BE、CF是△ABC的角平分线，BE、CF相交于D，∠ABC＝50°，∠ACB＝70°，则∠CDE的度数是（ ）
A、50° B、60° C、70° D、120°7. 如图，AD是△ABC的角平分线，过点D作DE⊥AB于E，DF⊥AC于F，则下列结论：①DE＝DF；②BD＝CD；③AE＝AF；④∠ADE＝∠ADF，其中正确结论的个数有（ ）
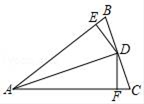A、1个 B、2个 C、3个 D、4个8. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一矩形如图，通过计算两个图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
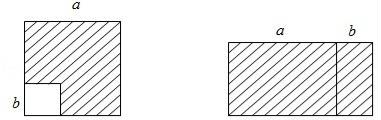A、（a﹣b）（a+2b）＝a2﹣2b2+ab B、（a+b）2＝a2+2ab+b2 C、（a﹣b）2＝a2﹣2ab+b2 D、（a﹣b）（a+b）＝a2﹣b29. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1 ， P2 ， P3 ， P4四个点中找出符合条件的点P，则点P有（ ）
A、1个 B、2个 C、3个 D、4个10. 已知3m＝a，81n＝b，m、n为正整数，则33m+12n的值为（ ）A、a3b3 B、15ab C、3a+12b D、a3+b3二、填空题
-
11. 计算：（x﹣2）（2+x）＝.12. 八边形中过其中一个顶点有条对角线.13. 如图，△ABC≌△DEF，则∠E的度数为.
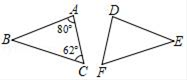14. 如果等腰三角形的两边长分别为3和7，那么它的周长为.15. 若x2+kx﹣15＝（x+3）（x+b），则k＝.16. 若一个多边形的每一个内角都等于156°，则这个多边形是边形.17. 若x2+2（m﹣4）x+25是一个完全平方式，那么m的值应为.18. 如图，在△ABC中，∠C=46°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1﹣∠2的度数是.
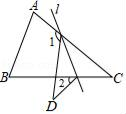19. 如图，在△ABD中，∠BAD＝80°，C为BD延长线上一点，∠BAC＝130°，△ABD的角平分线BE与AC交于点E，连接DE，则∠DEB＝.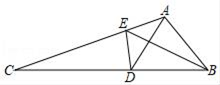
三、解答题
-
20.
(1)、计算：（﹣4x）（2x2+3x﹣1）
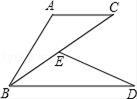
(2)、解方程：（2x﹣3）（3x﹣2）＝6（x﹣2）（x+2）21. 已知：如图，E为BC上一点，AC∥BD，AC＝BE，BC＝BD.求证：AB＝DE.
22. 已知：如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E.若∠C＝28°，求∠DAE的度数.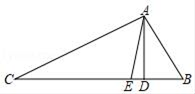
23. 已知x2+y2＝25，x+y＝7，求xy和x﹣y的值.24. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图所示）就是一例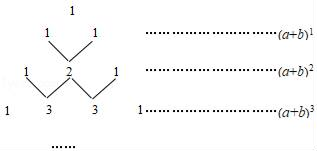
这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方（左右）两数之和.事实上，这个三角形给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律.例如，在三角形中第三行的三个数1、2、1，恰好对应（a+b）2＝a2+2ab+b2展开式中各项的系数；第四行的四个数1、3、3、1，恰好对应着（a+b）3＝a3+3a2b+3ab2+b3展开式中各项的系数等等.
(1)、根据上面的规律，（a+b）4展开式的各项系数中最大的数为；(2)、直接写出25+5×24×（﹣3）+10×23×（﹣3）2+10×22×（﹣3）3+5×2×（﹣3）4+（﹣3）5的值；(3)、若（2x﹣1）2018＝a1x2018+a2x2017+a3x2016+……+a2017x2+a2018x+a2019 ， 求a1+a2+a3+……+a2017+a2018的值.25. 如图，在△ABC中，BC＝10，BC边上的高为3.将点A绕点B逆时针旋转90°得到点E，绕点C顺时针旋转90°得到点D.沿BC翻折得到点F，从而得到一个凸五边形BFCDE，则五边形BFCDE的面积为.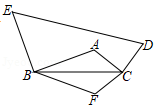
26.
(1)、计算：（x3）2+x3•x5÷x2﹣（2x2）3
(2)、化简：[（x+2y）2﹣（x+y）（3x﹣y）﹣5y2]÷2x.27. 如图，在等腰Rt△ABC中，∠ACB＝90°，∠CBA＝∠CAB，AC＝BC.点D在CB的延长线上，BD＝CB.DF⊥BC，点E在BC的延长线上，EC＝FD.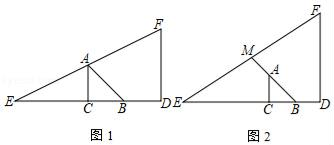
(1)、如图1，若点E、A、F三点共线，求证：∠FAB＝∠FBA；(2)、如图2，若线段EF与BA的延长线交于点M，求证：EM＝FM.28. 已知：平面直角坐标系中，点A（a，b）的坐标满足|a﹣b|+b2﹣8b+16＝0.
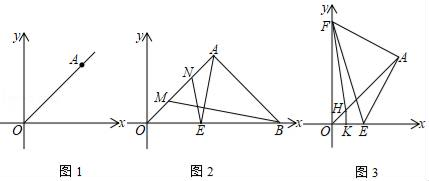(1)、如图1，求证：OA是第一象限的角平分线；(2)、如图2，过A作OA的垂线，交x轴正半轴于点B，点M、N分别从O、A两点同时出发，在线段OA上以相同的速度相向运动（不包括点O和点A），过A作AE⊥BM交x轴于点E，连BM、NE，猜想∠ONE与∠NEA之间有何确定的数量关系，并证明你的猜想；(3)、如图3，F是y轴正半轴上一个动点，连接FA，过点A作AE⊥AF交x轴正半轴于点E，连接EF，过点F点作∠OFE的角平分线交OA于点H，过点H作HK⊥x轴于点K，求2HK+EF的值.