湖北省武汉市江岸区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-10-21 类型:期中考试
一、单选题
-
1. 下列国产汽车车标不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下长度的三条线段,不能组成三角形的是( )A、3、8、2 B、2、5、4 C、6、3、5 D、9、15、73. 五边形的外角和等于( )
2. 以下长度的三条线段,不能组成三角形的是( )A、3、8、2 B、2、5、4 C、6、3、5 D、9、15、73. 五边形的外角和等于( )
A、180° B、360 ° C、540° D、720°4. 如图,要在三条交错的公路区域附近修建一个物流公司仓库,使仓库到三条公路的距离相等,则可以选择的地址有( )处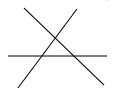 A、1 B、2 C、3 D、45. 已知图中的两个三角形全等,则∠
A、1 B、2 C、3 D、45. 已知图中的两个三角形全等,则∠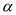 度数是( )
度数是( ) 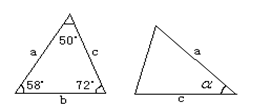 A、72° B、60° C、58° D、50°6. 已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )A、50° B、80° C、50°或80° D、40°或65°7. 下列给出的各组条件中,不能使 的是( )A、 , , B、 , , C、 , , D、 , ,8. 如图,在 的边 上取一点 使 ,作 于 ,作 交 于点 ,则 与 的关系是( )
A、72° B、60° C、58° D、50°6. 已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )A、50° B、80° C、50°或80° D、40°或65°7. 下列给出的各组条件中,不能使 的是( )A、 , , B、 , , C、 , , D、 , ,8. 如图,在 的边 上取一点 使 ,作 于 ,作 交 于点 ,则 与 的关系是( )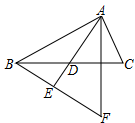 A、 B、 C、 D、9. 如图,点 是 的角平分线 上一点,于点 ,点 是线段 上一点.已知 , ,点 为 上一点.若满足 ,则 的长度为( )
A、 B、 C、 D、9. 如图,点 是 的角平分线 上一点,于点 ,点 是线段 上一点.已知 , ,点 为 上一点.若满足 ,则 的长度为( )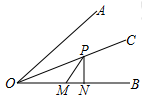 A、3 B、4 C、5 D、3或510. 如图, 中, , , , , 垂直平分 ,点 为 的延长线上一点,满足 ,则 ( )
A、3 B、4 C、5 D、3或510. 如图, 中, , , , , 垂直平分 ,点 为 的延长线上一点,满足 ,则 ( )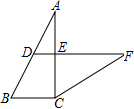 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
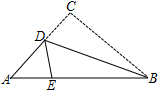
11. 点 关于 轴的对称点 的坐标是.12. 一个六边形的内角和是.13. 如图的三角形纸片中, , , .点 是 上一点,沿过 折叠,使点 落在 上的点 处,则 的周长为 .
 14. 等腰三角形有一个角等于30度,则底边上的高和一腰上的高所在直线相交形成的锐角等于度.15. 如图,正五边形 ,连接 、 、 ,则图中的等腰三角形共有个.
14. 等腰三角形有一个角等于30度,则底边上的高和一腰上的高所在直线相交形成的锐角等于度.15. 如图,正五边形 ,连接 、 、 ,则图中的等腰三角形共有个.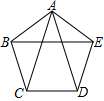 16. 如图,直线 直线 于点 ,点 、点 是直线 上的点,作 直线 且 ,作 直线 于点 ,在射线 上取一点 ,使 , 的延长线交直线 于点 .若 ,则 .
16. 如图,直线 直线 于点 ,点 、点 是直线 上的点,作 直线 且 ,作 直线 于点 ,在射线 上取一点 ,使 , 的延长线交直线 于点 .若 ,则 .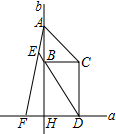
三、解答题
-
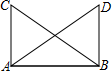
17. 如图, , , ,求证: .
 18. 等腰三角形的一个角比另一个角大 ,求等腰三角形的顶角的度数.19. 如图, , 与 相邻的外角的平分线相交于点 .
18. 等腰三角形的一个角比另一个角大 ,求等腰三角形的顶角的度数.19. 如图, , 与 相邻的外角的平分线相交于点 .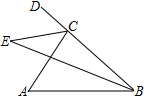 (1)、已知 , ,求 的度数.(2)、直接写出 与 的数量关系.20. 如图所示, 在平面直角坐标系中(每个小正方形的边长为1个单位长度)
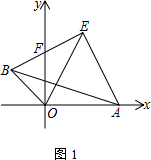
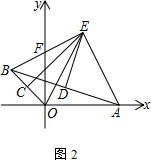
(1)、已知 , ,求 的度数.(2)、直接写出 与 的数量关系.20. 如图所示, 在平面直角坐标系中(每个小正方形的边长为1个单位长度)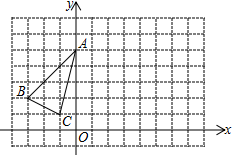 (1)、直接写出点 的坐标;(2)、画出 关于 轴对称的 ;(3)、将 向右平移8个单位,画出平移后的 ,指出 与 位置关系.21. 中, , 、 是 的三等分线.
(1)、直接写出点 的坐标;(2)、画出 关于 轴对称的 ;(3)、将 向右平移8个单位,画出平移后的 ,指出 与 位置关系.21. 中, , 、 是 的三等分线.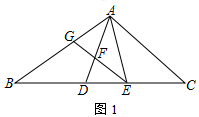
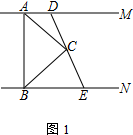
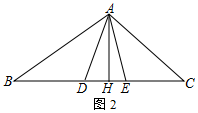 (1)、如图, 平分 分别交 、 于 、 ,求证: .(2)、如图, 是 的高,判断 与 的数量关系,并说明理由.22. 如图,将 沿 翻折,使点 落在 上的点 处.
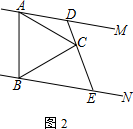
(1)、如图, 平分 分别交 、 于 、 ,求证: .(2)、如图, 是 的高,判断 与 的数量关系,并说明理由.22. 如图,将 沿 翻折,使点 落在 上的点 处.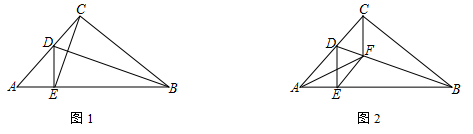 (1)、连接 ,求证: 垂直平分 ;(2)、作 平分 交 于点 ,连接 、 ,求证: .
(1)、连接 ,求证: 垂直平分 ;(2)、作 平分 交 于点 ,连接 、 ,求证: .