湖北省武汉市蔡甸区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-21 类型：期中考试
一、单选题
-
1. 若三角形的三边长分别为3，4，x﹣1，则x的取值范围是（ ）A、0＜x＜8 B、2＜x＜8 C、0＜x＜6 D、2＜x＜62. 如图所示，一个直角三角形纸片，剪去这个直角后，得到一个四边形，则∠1+∠2的度数为（ ）
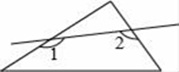A、150° B、180° C、240° D、270°3. 已知凸n边形有n条对角线，则此多边形的内角和是（ ）A、360° B、540° C、720° D、900°4. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）
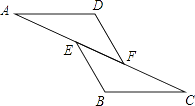A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC5. 如图，在∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是（ ）
A、SSS B、SAS C、AAS D、HL6. 如图，在3×3的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中最多能画出（ ）个格点三角形与△ABC成轴对称.
A、6个 B、5个 C、4个 D、3个7. 如图，点O是△ABC内一点，∠A=80°，BO、CO分别是∠ABC和∠ACB的角平分线，则∠BOC等于（ ）
A、140° B、120° C、130° D、无法确定8. 小明把一副 的直角三角板如图摆放，其中 ，则 等于（ ）
A、 B、 C、 D、9. 如图，在△ACD和△BCE中，AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P，则∠BPD的度数为（ ）
A、120° B、125° C、130° D、155°10. 如图，在△ABC中，E为AC的中点，AD平分∠BAC，BA：CA=2：3，AD与BE相交于点O，若△OAE的面积比△BOD的面积大1，则△ABC的面积是（ ）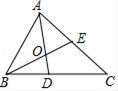
A、8 B、9 C、10 D、11二、填空题
-
11. 凸多边形的外角和等于.12. 点A(a，5)，B(3，b)关于y轴对称，则a+b＝.13. 如图，D在BC边上，△ABC≌△ADE，∠EAC=40°，则∠ADE的度数为.
14. 如图，在△ABC中，AD是高，AE平分∠BAC，∠B=50°，∠C=80°，则∠DAE=.
15. 如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法中正确的序号是.①△ABE的面积等于△BCE的面积；②∠AFG=∠AGF；③∠FAG=2∠ACF；④BH=CH.
16. 如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，若∠A=60°，则∠BMN的度数是.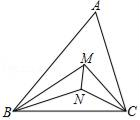
三、解答题
-
17. 已知：一个多边形的内角和是外角和的2倍，这个多边形是几边形？18. 如图，点B、E、C、F在同一直线上，BE=CF，AB=DE，AC=DF．
求证：AB∥DE．
19. 如图，点E在AB上，△ABC≌△DEC，求证：CE平分∠BED．
20. 如图，AD为△ABC的中线，F在AC上，BF交AD于E，且BE=AC.求证：AF=EF.
21. 如图所示，AB>AC，∠A的平分线与BC的垂直平分线相交于点D，作DE⊥AB于点E，DF⊥AC于点F.求证：BE=CF.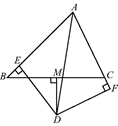
22. 如图，在平面直角坐标系中有一个轴对称图形，A（3，-2），B（3，﹣6）两点在此图形上且互为对称点，若此图形上有一个点C（﹣2，+1）.
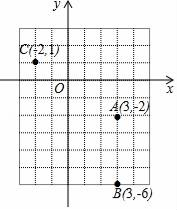(1)、求点C的对称点的坐标.(2)、求△ABC的面积.
