湖北省沙洋县2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-10-21 类型：期中考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 点M（﹣3，2）关于y轴对称的点的坐标为（ ）A、（﹣3，﹣2） B、（3，﹣2） C、（3，2） D、（﹣3，2）3. 已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为( )
A、2 B、3 C、5 D、134. 如图，已知：MA∥NC，MB∥ND，MB＝ND.则△MAB≌△NCD的理由是（ ）
A、边边边 B、边角边 C、角角边 D、边边角5. 一个多边形的内角和为540°，则它的对角线共有（ ）A、3条 B、5条 C、6条 D、12条6. 一个等腰三角形的两边长分别为2和5，则它的周长为（ ）A、7 B、9 C、12 D、9或127. 已知AD是△ABC的一条高，∠BAD＝70°，∠CAD＝20°，则∠BAC的度数为（ ）A、50° B、60° C、90° D、50°或90°8. 在平面直角坐标系中，O为坐标原点，点A的坐标为（2，2），M为X轴上一点，且使得△MOA为等腰三角形，则满足条件的点M的个数为（ ）A、2 B、3 C、4 D、59. 在下列条件中，能判定△ABC和△A′B′C′全等的是（ ）A、AB＝A′B′，BC＝B′C′，∠A＝∠A′ B、∠A＝∠A′，∠C＝∠C′，AC＝B′C′ C、∠A＝∠A′，∠B＝∠B′，∠C＝∠C′ D、AB＝A′B′，BC＝B′C′，∠B＝∠B′.10. 如图，已知△ABC中，∠ABC＝45°，F是高AD和BE的交点，∠CAD＝30°，CD＝4，则线段BF的长度为（ ）
A、6 B、7 C、8 D、911. 如图2，AB=AC，BE⊥AC于E，CF⊥AB于F，BE，CF交于D，则以下结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上.正确的是（ ）
A、① B、② C、①② D、①②③12. 下列命题：①面积相等的两个三角形全等；②三角形三条高所在的直线交于一点；③等腰三角形两底角的平分线相等；④等腰三角形边上的高、中线和对角的平分线互相重合.其中真命题有（ ）个.A、1 B、2 C、3 D、4.二、填空题
-
13. 如图，为了使矩形相框不变形，通常可以相框背后加根木条固定.这种做法体现的数学原理是.
14. 等腰三角形腰上的高与另一腰的夹角为30°，则底角度数是或.15. 如图，在 中，CD平分∠ACB，DE∥BC，DE交AC于E，若DE=7，AE=5，则AC=。
16. 如图所示，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为.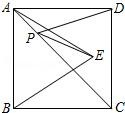
17. 如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：①AP＝CE；②∠PME＝60°；③BM平分∠AME；④AM+MC＝BM，其中正确的有（填序号）.
三、解答题
-
18. 如图，有两条国道相交于点O，在∠AOB的内部有两个村庄C、D，现要修建一加油站P，使点P到OA、OB的距离相等，且PC＝PD，用尺规作图，作出加油站的位置（保留作图痕迹，不写作法）
19. 如图，点E、C在BF上，BE＝CF，AB＝DE，∠B＝∠DEF.求证：AC＝DF，AC∥DF.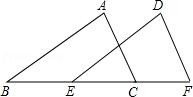
20. 如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0），C（﹣1，0）.
(1)、将△ABC向右平移5个单位，再向下平移4个单位得△A1B1C1 ， 图中画出△A1B1C1 ， 平移后点A的对应点A1的坐标是.(2)、将△ABC沿x轴翻折△A2BC，图中画出△A2BC，翻折后点A对应点A2坐标是.(3)、将△ABC向左平移2个单位，则△ABC扫过的面积为.21. 如图，△ABC为等边三角形，D、E分别是边AC、BC上的点，且AD＝CE，AE与BD相交于点P.
(1)、求∠BPE的度数；(2)、若BF⊥AE于点F，试判断BP与PF的数量关系并说明理由.22. 在△ABC中，AB＞BC，AB＝AC，DE是AB的垂直平分线，垂足为D，交AC于E.
(1)、若∠ABE＝40°，求∠EBC的度数；(2)、若△ABC的周长为41cm，一边长为15cm，求△BCE的周长.
