河南省南召县2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2019-10-21 类型：期中考试

进入出卷网下载

一、单选题

1. 64的立方根是（　　）

A、4 B、±4 C、8 D、±8

查看试题解析
2. 计算(-a)²·a³结果是（）

A、a⁶ B、a⁵ C、-a⁶ D、-a⁵

查看试题解析
3. 下列各式正确的是（）

A、± $\sqrt[3]{1}$ ＝±1 B、 $\sqrt{4}$ ＝±2 C、 $\sqrt{{(- 6)}^{2}}$ ＝－6 D、 $\sqrt[3]{- 27}$ ＝3

查看试题解析
4. 下列各式中，不能用平方差公式计算的是（）

A、 $(x - y) (- x + y)$ B、 $(- x + y) (- x - y)$ C、 $(- x - y) (x - y)$ D、 $(x + y) (- x + y)$

查看试题解析
5. 下列计算结果正确的是（）

A、 $a^{8} \div a^{4} = a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a^{3})}^{2} = a^{6}$ D、 ${(- 2 a^{2})}^{3} = 8 a^{6}$

查看试题解析
6. 下列各式中，一定成立的是（）

A、 ${(x + y)}^{2} = x^{2} + y^{2}$ B、 $(x + 6) (x - 6) = x^{2} - 6$ C、 ${(x - y)}^{2} = {(y - x)}^{2}$ D、 $(3 x - y) (- 3 x + y) = 9 x^{2} - y^{2}$

查看试题解析
7. 计算 $∣ \sqrt{6} - 3 ∣ + ∣ 2 - \sqrt{6} ∣$ 的值为（）

A、 $5$ B、 $5 - 2 \sqrt{6}$ C、 $1$ D、 $2 \sqrt{6} - 1$

查看试题解析
8.
如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为（　　）

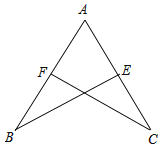A、2 B、3 C、5 D、2.5

查看试题解析
9. 如图，△ABC≌△DEF，∠A=50°，∠E=100°，则∠F的度数是（）

A、 $30^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $100^{\circ}$

查看试题解析
10. 由 $m (a + b + c) = ma + mb + mc$ ，可得：
$(a + b) (a^{2} - ab + b^{2}) = a^{3} - a^{2} b + {ab}^{2} + a^{2} b - {ab}^{2} + b^{3} = a^{3} + b^{3}$ ，
即 $(a + b) (a^{2} - ab + b^{2}) = a^{3} + b^{3}$ ．①
我们把等式①叫做多项式乘法的立方公式．
下列应用这个立方公式进行的变形不正确的是（）

A、 $(x + 4 y) (x^{2} - 4 xy + 16 y^{2}) = x^{3} + 64 y^{3}$ B、 $(2 x + y) (4 x^{2} - 2 xy + y^{2}) = 8 x^{3} + y^{3}$ C、 $x^{3} + 27 = (x + 3) (x^{2} - 3 x + 9)$ D、 $(a + 1) (a^{2} + a + 1) = a^{3} + 1$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{8}$ ﹣|﹣2|＝.

查看试题解析
12. 计算： ${xy}^{2} \cdot (- \frac{1}{2} x^{2}) =$ ．

查看试题解析
13. 已知 $m^{2} - n^{2} = 16$ ， $m + n = 5$ ，则 $m - n =$ ．

查看试题解析
14. 如图， $∠ A = ∠ C$ ，只需补充一个条件：，就可得△ABD≌△CDB.

查看试题解析
15. 如图， $D$ 为 $Rt △ ABC$ 中斜边 $BC$ 上的一点，且 $BD = AB$ ，过点 $D$ 作 $BC$ 的垂线，交 $AC$ 于点 $E$ ，若 $AE = 12 cm$ ，则 $DE$ 的长为 $cm$ .

查看试题解析

三、解答题

16. 计算： ${(- 2 x)}^{2} + (6 x^{3} - 12 x^{4}) \div 3 x^{2}$ .

查看试题解析
17. 计算： ${(3 x^{2})}^{2} \cdot (- 4 y^{3}) \div {(6 xy)}^{2}$ .

查看试题解析
18. 分解因式： $- a^{3} + 4 a^{2} b - 4 a b^{2}$ .

查看试题解析
19. 化简求值： $[{(x + 2 y)}^{2} - (x + y) (3 x - y) - 5 y^{2}] \div (- 2 x)$ ；其中x=-2； $y = - \frac{1}{2}$ .

查看试题解析
20. 如图，在四边形ABCD中，对角线AC、BD交于点O，且OA=OC，OB=OD.

(1)、直接写出图中的全等三角形（写出3对即可）；

(2)、直接写出你发现的其他结论（写出3条即可）.

查看试题解析
21. 如图，△ABC与△ABD中，AD与BC相交于O点，∠1=∠2，请你添加一个条件（不再添加其它线段，不再标注或使用其他字母），使AC=BD，并给出证明.
你添加的条件是：

证明：

查看试题解析
22. 阅读理解：
例：已知： $m^{2} + 2 mn + 2 n^{2} - 6 n + 9 = 0$ ，

求： $m$ 和 $n$ 的值.

解： $∵$ $m^{2} + 2 mn + 2 n^{2} - 6 n + 9 = 0$ ，

$∴$ $m^{2} + 2 mn + n^{2} + n^{2} - 6 n + 9 = 0$ ，

$∴$ ${(m + n)}^{2} + {(n - 3)}^{2} = 0$ ，

$∴$ $m + n = 0$ ， $n - 3 = 0$ ，

$∴$ $m = - 3$ ， $n = 3$ ，

解决问题：

(1)、若 $x^{2} - 4 xy + 5 y^{2} + 2 y + 1 = 0$ ，求x、y的值；

(2)、已知 $a$ ， $b$ ， $c$ 是 $△ ABC$ 的三边长且满足 $a^{2} + b^{2} = 10 a + 12 b - 61$ ，
①直接写出a=.b=.

②若 $c$ 是 $△ ABC$ 中最短边的边长（即c<a；c<b），且 $c$ 为整数，直接写出 $c$ 的值可能是.

查看试题解析
23. 如图，已知 $△ ABC$ 中， $AB = AC = 24$ 厘米， $∠ ABC = ∠ ACB$ ， $BC = 16$ 厘米，点 $D$ 为 $AB$ 的中点.如果点 $P$ 在线段 $BC$ 上以 $4$ 厘米/秒的速度由 $B$ 点向 $C$ 点运动.同时，点 $Q$ 在线段 $CA$ 上由 $C$ 点以 $a$ 厘米/秒的速度向 $A$ 点运动.设运动的时间为 $t$ 秒.

(1)、直接写出：
①BD＝厘米；②BP＝厘米；

③CP＝厘米；④CQ＝厘米；

（可用含 $t$ 、a的代数式表示）

(2)、若以 $D$ ， $B$ ， $P$ 为顶点的三角形和以 $P$ ， $C$ ， $Q$ 为顶点的三角形全等，试求 $a$ 、t的值；

(3)、若点 $Q$ 以（ $2$ ）中的运动速度从点 $C$ 出发，点 $P$ 以原来的运动速度从点 $B$ 同时出发，都逆时针沿 $△ ABC$ 三边运动.设运动的时间为 $t$ 秒；直接写出t=秒时点 $P$ 与点 $Q$ 第一次相遇.

查看试题解析