河南省洛阳市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-10-21 类型:期中考试
一、单选题
-
1. 下列图形是轴对称图形的有( )
 A、2个 B、3个 C、4个 D、5个2. 十边形的内角和为( )度.A、1800 B、1260 C、1440 D、16203. 已知△ABC≌△DEF,且△ABC周长为100,AB=35,DF=30,则EF的长为( )A、25 B、30 C、35 D、404. 等腰三角形的周长为17,则它的腰长可能为( )A、8 B、9 C、4 D、35. 在下列图形中,正确画出△ABC的AC边上的高的图形是( )A、
A、2个 B、3个 C、4个 D、5个2. 十边形的内角和为( )度.A、1800 B、1260 C、1440 D、16203. 已知△ABC≌△DEF,且△ABC周长为100,AB=35,DF=30,则EF的长为( )A、25 B、30 C、35 D、404. 等腰三角形的周长为17,则它的腰长可能为( )A、8 B、9 C、4 D、35. 在下列图形中,正确画出△ABC的AC边上的高的图形是( )A、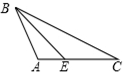 B、
B、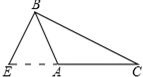 C、
C、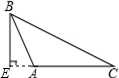 D、
D、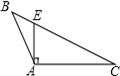 6. 如图,小明把一块三角形玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,则最省事的方法是带第③块去,理由是根据全等的判定定理( )
6. 如图,小明把一块三角形玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,则最省事的方法是带第③块去,理由是根据全等的判定定理( )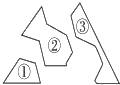 A、SAS B、AAS C、SSS D、ASA7. 若三角形ABC中,三个内角度数的比为3:5:8,则三角形ABC是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形8. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
A、SAS B、AAS C、SSS D、ASA7. 若三角形ABC中,三个内角度数的比为3:5:8,则三角形ABC是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形8. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )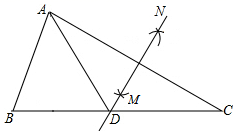 A、 B、 C、 D、9. 如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
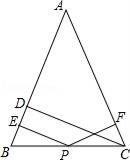
A、 B、 C、 D、9. 如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )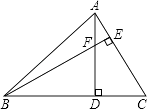 A、4cm B、6cm C、8cm D、9cm10. 如图,将矩形纸片ABCD(图1)按如下步骤操作:
A、4cm B、6cm C、8cm D、9cm10. 如图,将矩形纸片ABCD(图1)按如下步骤操作:( 1 )以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为( )
 A、60° B、67.5° C、72° D、75°
A、60° B、67.5° C、72° D、75°二、填空题
-
11. 已知整数a,b,c是△ABC的三条边长,若a=1,b=5,则奇数c=.12.
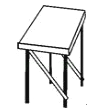
如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
 13. 如图,正五角星的每个角都是顶角为36°的等腰三角形,则∠ 等于.
13. 如图,正五角星的每个角都是顶角为36°的等腰三角形,则∠ 等于.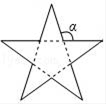 14. 如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为.
14. 如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为.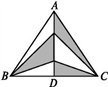 15. 如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
15. 如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.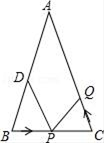
三、解答题
-
16. 已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.17. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
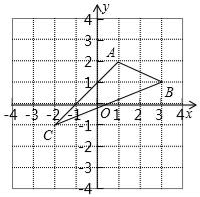 (1)、在图中作出△ABC关于 轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标(直接写答案):A1 , B1 , C1.18. 如图,在△ABC中,点D在边BC上,若AB=AD=CD,∠BAD=100°,求∠C度数.
(1)、在图中作出△ABC关于 轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标(直接写答案):A1 , B1 , C1.18. 如图,在△ABC中,点D在边BC上,若AB=AD=CD,∠BAD=100°,求∠C度数.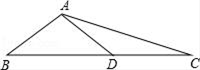 19. 四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.
19. 四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.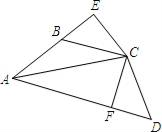
求证:
(1)、△CBE≌△CDF;(2)、AB+DF=AF.20. 如图,在等边△ABC中,AB=4,角BAC的平分线交BC于点D,M为AB边中点,N是AD上的动点.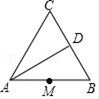
①在图上作出使得BN+MN的和最小时点N的位置,并说明理由.
②求出BN+MN的最小值.(提示:Rt△ABC中,∠C=90°,则有AC2+BC2=AB2成立)
21. 如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.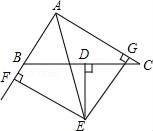
求证:
(1)、BF=CG;(2)、AB+AC=2AF.