江苏省泰州市医药高新区2020届九年级上学期数学第一次月考试卷
试卷更新日期:2019-10-21 类型:月考试卷
一、单选题
-
1. 下列方程中一定是一元二次方程的是( )A、5x2- +2=0 B、ax2+bx+c=0 C、2x+3=6 D、(a2+2)x2-2x+3=02. 要使分式 的值为0,则x应该等于( )A、4或1 B、4 C、1 D、-4或-13. 设 , 是方程 的两个实数根,则 的值为( )A、 B、 C、 D、4. 自行车车轮要做成圆形,主要是根据圆的以下哪个特征( )A、圆是轴对称图形 B、圆是中心对称图形 C、圆上各点到圆心的距离相等 D、直径是圆中最长的弦5. 如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2 ,AB=1,则△PAB周长的最小值是( )
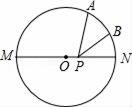 A、2 +1 B、 +1 C、2 D、3
A、2 +1 B、 +1 C、2 D、3二、填空题
-
6. 某商品原价169元,经连续两次降价后售价为121元,设平均每次降价的百分率为x,则可列方程为.7. 内角和等于外角和2倍的多边形是边形.8. 已知三角形的边长分别为6,8,10,则它的外接圆的半径是.9. 已知 ,则 的值为.10. 已知等腰三角形的一边长为9,另一边长为方程x2-8x+15=0的根,则该等腰三角形的周长为.11. 如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5 cm,小圆的半径为3 cm,则弦AB的长为cm.
 12. 已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是.13. 若点O是△ABC的外心,且∠BOC=70°,则∠BAC的度数为.14. 对于两个不相等的实数a、b,我们规定符号minh{a,b}表示a、b中较小的数的一半,如minh{2,3}=1.按照这个规定,方程minh{x,-x}= 的解为.15. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有两个交点,则r的取值范围是.
12. 已知圆O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是.13. 若点O是△ABC的外心,且∠BOC=70°,则∠BAC的度数为.14. 对于两个不相等的实数a、b,我们规定符号minh{a,b}表示a、b中较小的数的一半,如minh{2,3}=1.按照这个规定,方程minh{x,-x}= 的解为.15. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有两个交点,则r的取值范围是.三、解答题
-
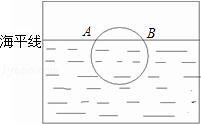
16. 解方程:(1)、(2)、17. 先化简,再求值: ,其中x满足方程 .18. 已知关于x的方程x2+4x+3-a=0.(1)、若此方程有两个不相等的实数根,求a的取值范围;(2)、在(1)的条件下,当a取满足条件的最小整数,求此时方程的解.19. 每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.
 20. 如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
20. 如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.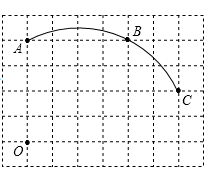 (1)、请完成如下操作:
(1)、请完成如下操作:①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系; ②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)、请在(1)的基础上,完成下列填空:①写出点的坐标:C、D;
②⊙D的半径=(结果保留根号);
③若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由.
21. 某商场推销一种书包,进价为30元,在试销中发现这种书包每天的销售量P(个)与每个书包销售价x(元)满足一次函数关系式.当定价为35元时,每天销售30个;定价为40元时,每天销售20个.(1)、求P关于x的函数关系式;(2)、如果要保证商场每天销售这种书包获利200元,求书包的销售单价应定为多少元?22. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.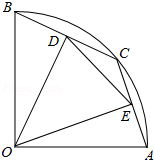 (1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.23. 如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.
(1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.23. 如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E. (1)、求证:AB=AC.(2)、若BD=11,DE=2,求CD的长.24. 如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)、求证:AB=AC.(2)、若BD=11,DE=2,求CD的长.24. 如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.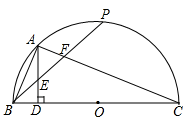 (1)、求证:AE=BE;(2)、判断BE与EF是否相等吗,并说明理由;(3)、小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB不符合题意的关系式.25. 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程 是关于x的一元二次方程.(1)、判断方程 的根的情况为(填序号);
(1)、求证:AE=BE;(2)、判断BE与EF是否相等吗,并说明理由;(3)、小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB不符合题意的关系式.25. 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程 是关于x的一元二次方程.(1)、判断方程 的根的情况为(填序号);①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
(2)、如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程 的根;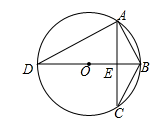 (3)、若 是方程 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
(3)、若 是方程 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.