2017年江苏省连云港市中考数学试卷
试卷更新日期:2017-07-06 类型:中考真卷
一、选择题
-
1. 2的绝对值是( )A、﹣2 B、2 C、﹣ D、2. 计算a•a2的结果是( )A、a B、a2 C、2a2 D、a33. 小广,小娇分别统计了自己近5次数学测试成绩,下列统计量中能用来比较两人成绩稳定性的是( )A、方差 B、平均数 C、众数 D、中位数4. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
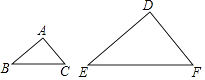 A、 = B、 = C、 = D、 =5. 由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图,左视图和俯视图的面积,则( )
A、 = B、 = C、 = D、 =5. 由6个大小相同的正方体搭成的几何体如图所示,比较它的正视图,左视图和俯视图的面积,则( )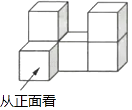 A、三个视图的面积一样大 B、主视图的面积最小 C、左视图的面积最小 D、俯视图的面积最小6. 关于 的叙述正确的是( )A、在数轴上不存在表示 的点 B、 = + C、 =±2 D、与 最接近的整数是37. 已知抛物线y=ax2(a>0)过A(﹣2,y1)、B(1,y2)两点,则下列关系式一定正确的是( )A、y1>0>y2 B、y2>0>y1 C、y1>y2>0 D、y2>y1>08.
A、三个视图的面积一样大 B、主视图的面积最小 C、左视图的面积最小 D、俯视图的面积最小6. 关于 的叙述正确的是( )A、在数轴上不存在表示 的点 B、 = + C、 =±2 D、与 最接近的整数是37. 已知抛物线y=ax2(a>0)过A(﹣2,y1)、B(1,y2)两点,则下列关系式一定正确的是( )A、y1>0>y2 B、y2>0>y1 C、y1>y2>0 D、y2>y1>08.如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
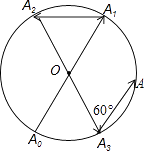 A、4 B、2 C、2 D、0
A、4 B、2 C、2 D、0二、填空题
-
9. 分式 有意义的x的取值范围为 .10. 计算(a﹣2)(a+2)= .11. 截至今年4月底,连云港市中哈物流合作基地累计完成货物进、出场量6800000吨,数据6800000用科学记数法可表示为 .12. 已知关于x的方程x2﹣2x+m=0有两个相等的实数根,则m的值是 .13. 如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B= .
 14. 如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径长为 .
14. 如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径长为 .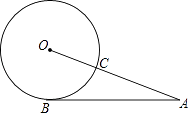 15. 设函数y= 与y=﹣2x﹣6的图象的交点坐标为(a,b),则 + 的值是 .16.
15. 设函数y= 与y=﹣2x﹣6的图象的交点坐标为(a,b),则 + 的值是 .16.如图,已知等边三角形OAB与反比例函数y= (k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则 的值为 . (已知sin15°= )
三、解答题
-
17. 计算:﹣(﹣1)﹣ +(π﹣3.14)0 .18. 化简 • .
19. 解不等式组 .20.某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段
频数
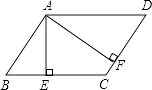
频率
60≤x<70
18
0.36
70≤x<80
17
c
80≤x<90
a
0.24
90≤x≤100
b
0.06
合计
1
根据以上信息解答下列问题:
 (1)、统计表中c的值为;样本成绩的中位数落在分数段中;(2)、补全频数分布直方图;(3)、若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?21. 为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.(1)、直接写出甲投放的垃圾恰好是A类的概率;(2)、求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.22. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)、统计表中c的值为;样本成绩的中位数落在分数段中;(2)、补全频数分布直方图;(3)、若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?21. 为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.(1)、直接写出甲投放的垃圾恰好是A类的概率;(2)、求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.22. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.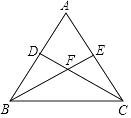 (1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.23.
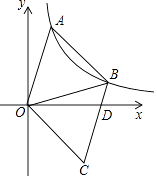
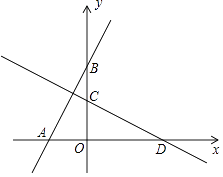
(1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.23.如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B,将直线AB绕着点顺时针旋转90°后,分别与x轴、y轴交于点D、C.
 (1)、若OB=4,求直线AB的函数关系式;(2)、连接BD,若△ABD的面积是5,求点B的运动路径长.24. 某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.(1)、若基地一天的总销售收入为y元,求y与x的函数关系式;(2)、试求如何分配工人,才能使一天的销售收入最大?并求出最大值.25.
(1)、若OB=4,求直线AB的函数关系式;(2)、连接BD,若△ABD的面积是5,求点B的运动路径长.24. 某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.(1)、若基地一天的总销售收入为y元,求y与x的函数关系式;(2)、试求如何分配工人,才能使一天的销售收入最大?并求出最大值.25.如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
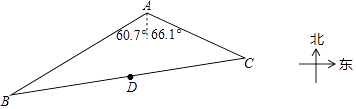 (1)、求△ABC的面积;(2)、景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(1)、求△ABC的面积;(2)、景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ≈1.414).
26.如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.
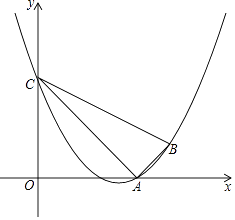 (1)、求此二次函数的关系式;(2)、判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;(3)、若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1 , △A1B1C1的外接圆记为⊙M1 , 是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.27.
(1)、求此二次函数的关系式;(2)、判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;(3)、若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1 , △A1B1C1的外接圆记为⊙M1 , 是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.27.问题呈现:
(Ⅰ)如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD . (S表示面积)
(Ⅱ)实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1 , 得到矩形A1B1C1D1 .
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+S .
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与S 之间的数量关系,并说明理由.
(Ⅲ)迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
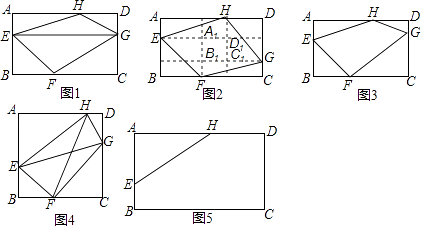
⑴如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF= ,求EG的长.

⑵如图5,在矩形ABCD中,AB=3,AD=5,点E、H分别在边AB、AD上,BE=1,DH=2,点F、G分别是边BC、CD上的动点,且FG= ,连接EF、HG,请直接写出四边形EFGH面积的最大值.
