浙江省杭州市余杭区2019-2020学年七年级上学期数学第一次月考试卷

试卷更新日期：2019-10-21 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 如果温度上升2℃记作+2℃，那么温度下降3℃记作（）

A、+2℃ B、﹣2℃ C、+3℃ D、﹣3℃

查看试题解析
2. 在 $\frac{1}{2}$ ，0，1，-9四个数中，负数是（）

A、 $\frac{1}{2}$ B、0 C、1 D、-9

查看试题解析
3. $- | - 2 |$ 的值为（）

A、2 B、-2 C、2或-2 D、 $\frac{1}{2}$

查看试题解析
4. 某市决定为全市中小学教室安装空调，今年预计投入资金126000000元，其中数字126000000用科学记数法可表示为（）

A、12.6×10⁷ B、1.26×10⁸ C、1.26×10⁹ D、0.126×10¹⁰

查看试题解析
5. 某种品牌的同一种洗衣粉有A、B、C三种袋装包装．每袋分别装有400克、300克、200克洗衣粉，售价分别为3.5元、2.8元、1.9元，A、B、C三种包装的洗衣粉每袋包装费用（含包装袋成本）分别为0.8元、0.6元、0.5元，厂家销售A、B、C三种包装的洗衣粉各1200千克，获得利润最大的是（）

A、A种包装的洗衣粉 B、B种包装的洗衣粉 C、C种包装的洗衣粉 D、三种包装的都相同

查看试题解析
6. 下列说法中，正确的是（）

A、(-3)²是负数 B、最小的有理数是零 C、若|x|=5，则x=5或-5 D、任何有理数的绝对值都是正数

查看试题解析
7. 实数a，b，c，d在数轴上的位置如图所示，下列关系式不正确的是（）

A、|a|＞|b| B、|ac|＝ac C、b＜d D、c+d＞0

查看试题解析
8. 下列各组数中，运算结果相等的是（）

A、 $（ \frac{2}{3} ）^{2}$ 与 $\frac{2^{2}}{3}$ B、-2²与（-2）² C、-（-1）⁷与-1⁷ D、（-5）³与-5³

查看试题解析
9. 小红的妈妈买了4筐白菜，以每筐25千克为标准，超过的千克数记为正数，不足的千克数记为负数，称重后的记录分别为+0.25，﹣1，+0.5，﹣0.75，小红快速准确地算出了4筐白菜的总质量为（）

A、﹣1千克 B、1千克 C、99千克 D、101千克

查看试题解析

10. 甲、乙、丙三人玩一种游戏，每玩一局都会将三人随机分成两组．积分方法举例说明：第一局甲、乙胜出，分别获得3分，丙获得-6分；第二局甲胜出获得12分，乙、丙分别获得-6分，两局之后的积分是：甲15分，乙3分，丙-12分．下表是三人的逐局积分统计表，计分错误开始于（）

	甲	乙	丙
第一局	3	3	-6
第二局	15	-3	-12
第三局	21	3	-24
第四局	15	-3	-12
第五局	12	-6	-6
第六局	0	18	12

A、第三局 B、第四局 C、第五局 D、第六局

查看试题解析

二、填空题（每小题4分，共24分）

11. 已知a>0，b<0，a+b>0，则a，b，-a，-b由小到大的排序是

查看试题解析
12. 一个数在数轴上所对应的点向左移动4个单位长度后，得到它的相反数的对应点，则这个数是．

查看试题解析
13. 一天早晨的气温是﹣8℃，中午上升了12℃，午夜又下降了10℃，午夜的气温是℃．

查看试题解析
14. “多少事，从来急；天地转，光阴迫．一万年太久，只争朝夕。”伟人毛泽东通过这首《满江红·和郭沫若同志》告诉我们青年学生：要珍惜每分每秒，努力工作，努力学习，一天时间为86400秒，数据86400用科学记数法表示为。

查看试题解析
15. 某校利用二维码进行学生学号统一编排．黑色小正方形表示1，白色小正方形表示0，将每一行数字从左到右依次记为a，b，c，d，那么利用公式a×2³+b×2²+c×2¹+d计算出每一行的数据．第一行表示年级，第二行表示班级，第三行表示班级学号的十位数，第四行表示班级学号的个位数．如图1所示，第一行数字从左往右依次是1，0，0，1，则表示的数据为1×2³+0×2²+0×2¹+1=9，计作09，第二行数字从左往右依次是1，0，1，0，则表示的数据为1×2³+0×2²+1×2¹=10，计作10，以此类推，图1代表的统一学号为091034，表示9年级10班34号．小明所对应的二维码如图2所示，则他的统一学号为．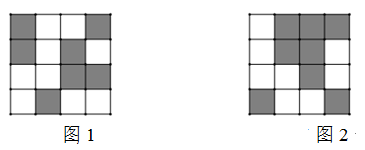

查看试题解析
16. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第2次将点A₁向右平移6个单位长度到达点A₂ ，第3次将点A₂向左移动9个单位长度到达点A₃…则第6次移动到点A₆时，点A₆在数轴上对应的实数是；按照这种规律移动下去，第2017次移动到点A₂₀₁₇时，A₂₀₁₇在数轴上对应的实数是.

查看试题解析

三、解答题（本大题有7小题，共66分）

17. 计算：

(1)、 $(- 3) + (- 4) - (+ 11) - (- 9)$

(2)、 $(\frac{2}{3} - \frac{1}{12} - \frac{1}{15}) \times (- 60)$

(3)、 $- 4 \div \frac{2}{3} - (- \frac{2}{3}) \times (- 30)$

(4)、 $- 1^{2} - \frac{3}{4} \times {[- 3^{3} \times {(\frac{2}{3})}^{2} + 2]}^{}^{}$

查看试题解析
18. 画一条数轴，并把 $- 4$ ， $- (- 3.5)$ ， $- 2 \frac{1}{2}$ ， $0$ ， $| - \frac{3}{2} |$ 各数在数轴上表示出来，再用“ $<$ ”把它们连接起来．

查看试题解析

19. “十·一”黄金周期间，我市某景点旅游区在7天假期中每天旅游的人数变化如下表：

（正数表示比前一天多的人数，负数表示比前一天少的人数）.（单位：万人）

日期	1日	2日	3日	4日	5日	6日	7日
人数变化	+ 1.2	+ 1.2	+ 0.4	– 0.2	– 0.8	+ 0.2	– 1.4

若9月30日的旅游人数记为3万人，则

(1)、请求出10月5日的旅游人数；

(2)、请判断7天内旅游人数最多的是哪一天？最少的是哪一天？它们相差多少万人？

(3)、若该景点门票为每人20元，请算出该景点黄金周期间的收入共多少万元？

查看试题解析

20. 已知a，b互为相反数，c与d互为倒数，m-1的绝对值是最小的正整数．
求： $\frac{a + b}{2019}$ -cd+m的值．

查看试题解析
21. 有一种“算24”的游戏，其规则是：任取四个1～13之间的自然数，将这四个数（每数只能用一次）进行加减乘除混合运算，其结果为24.例如2，3，4，5作运算.（5+3－2）×4=24，现有四个有理数3、4、－6、10，运用以上规则写出等于24的算式，你能写出几种算法?

查看试题解析
22. 某食品厂从生产的袋装食品中抽出样品 20 袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：

①这批样品的平均质量比标准质量多还是少？用你学过的方法合理解释；

②若标准质量为 450 克，则抽样检测的总质量是多少？

查看试题解析
23. 有理数a，b，c在数轴上的位置如图所示，且|a|=|b|．

(1)、求a+b与 $\frac{a}{b}$ 的值；

(2)、化简|c﹣a|+|c﹣b|+|a+b|

查看试题解析