浙江省杭州市余杭区2019-2020学年八年级上学期数学第一次月考试卷
试卷更新日期：2019-10-21 类型：月考试卷
一、选择题（每小题3分，共30分）
-
1. 如图，墙上钉着三根木条，a，b，c，量得∠1=70°，∠2=100°，那么木条a，b所在直线所夹的锐角是（ ）
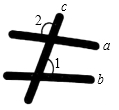A、5° B、10° C、30° D、70°2. 下列长度的3根小木棒不能搭成三角形的是（ ）A、2cm，3cm，4cm B、1cm，2cm，3cm C、3cm，4cm，5cm D、4cm，5cm，6cm3. 能说明命题“若|a|=|b|，则a=b”是假命题的反例为（ ）A、a=2,b=-2 B、a=1,b=0 C、a=1,b=1 D、a=-3,b=4. 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线。则对应作法错误的是（ ）
A、① B、② C、③ D、④5. 如图，△ABC≌△DEF，若 BC=12cm，BF=16cm，则下列判断错误的是（ ）
A、AB=DE B、BE=CF C、AB//DE D、EC=4cm6. 如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（ ）
A、40° B、45° C、50° D、60°7. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
8. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（ ）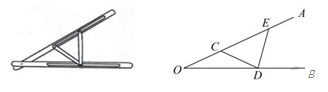
A、60° B、65° C、75° D、80°9. 将一根长24cm的筷子置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为h，则h的取值范围是（ ）
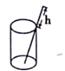A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm10. 如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，连结CE交AD于点F，连结BD交CE于点G，连结BE．下列结论中，正确的结论有（ ）
①CE=BD； ②△ADC是等腰直角三角形；③∠ADB=∠AEB；④S四边形BCDE= BD•CE；⑤BC2+DE2=BE2+CD2 ．
A、1个 B、2个 C、3个 D、4个二、填空题（每小题4分，共24分）
-
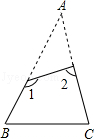
11. 如图，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1+∠2＝度.
12. 在△ABC中，∠A=50°，∠B=30°，点D在AB边上，连接CD，若△ACD为直角三角形，则∠BCD的度数为度．13. 定义：等腰三角形的顶角与其一个底角的度数的比值 称为这个等腰三角形的“特征值”.若等腰 中， ，则它的特征值 .14. 如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=度.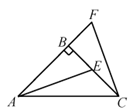
15. 已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA ， 垂足为点E ， 且直线DE交OB于点F ， 如图所示．若DE＝2，则DF＝ ．
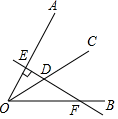16. 如图，在四边形 中， ．若将 沿 折叠，点 与边 的中点 恰好重合，则四边形 的周长为 ．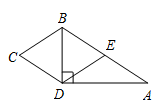
三、解答题（本大题有7小题，共66分）
-
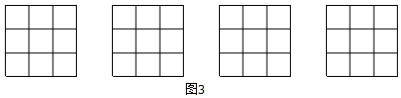
17. 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）
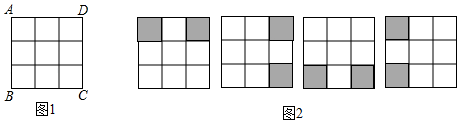
请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）
18. 如图，有两根长杆隔河相对，一杆高3m，另一杆高2m，两杆相距5m．两根长杆都与地面垂直，现两杆顶部各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮出一条小鱼，于是同时以同样的速度飞下来夺鱼，结果两只鱼鹰同时叼住小鱼．求两杆底部距小鱼的距离各是多少米．（假设小鱼在此过程中保持不动）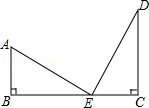
19. 如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F.
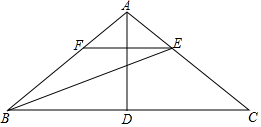(1)、若∠C＝36°，求∠BAD的度数；(2)、求证：FB＝FE.20. 在如图所示的网格中有四条线段AB、CD、EF、GH（线段端点在格点上），
(1)、选取其中三条线段，使得这三条线段能围成一个直角三角形．答：选取的三条线段为 ．
(2)、只变动其中两条线段的位置，在原图中画出一个满足上题的直角三角形（顶点仍在格点，并标上必要的字母）．答：画出的直角三角形为△ ．
(3)、所画直角三角形的面积为 ．21. 如图
(1)、问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则∠AEB的度数为 ， 线段AD、BE之间的关系 ．(2)、拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．①请判断∠AEB的度数，并说明理由；②当CM=5时，AC比BE的长度多6时，求AE的长．22. 如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•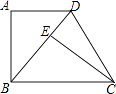
(1)、求证：△ABD≌△ECB；(2)、若∠EDC=65°，求∠ECB的度数；(3)、若AD=3，AB=4，求DC的长.23. 联想三角形外心的概念，我们可引入如下概念。定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。
举例：如图1，若PA=PB，则点P为△ABC的准外心。
应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD= AB，求∠APB的度数。
探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长。