2017年湖北省咸宁市中考数学试卷
试卷更新日期：2017-07-06 类型：中考真卷
一、选择题
-
1. 下表是我市四个景区今年2月份某天6时的气温，其中气温最低的景区是（ ）
景区
潜山公园
陆水湖
隐水洞
三湖连江
气温
﹣1℃
0℃
﹣2℃
2℃
A、潜山公园 B、陆水湖 C、隐水洞 D、三湖连江2. 在绿满鄂南行动中，咸宁市计划2015年至2017年三年间植树造林1210000亩，全力打造绿色生态旅游城市，将1210000用科学记数法表示为（ ）A、121×104 B、12.1×105 C、1.21×105 D、1.21×1063. 下列算式中，结果等于a5的是（ ）A、a2+a3 B、a2•a3 C、a5÷a D、（a2）34. 如图是某个几何体的三视图，该几何体是（ ）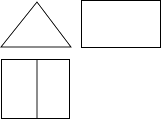
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥5. 由于受H7N9禽流感的影响，我市某城区今年2月份鸡的价格比1月份下降a%，3月份比2月份下降b%，已知1月份鸡的价格为24元/千克．设3月份鸡的价格为m元/千克，则（ ）A、m=24（1﹣a%﹣b%） B、m=24（1﹣a%）b% C、m=24﹣a%﹣b% D、m=24（1﹣a%）（1﹣b%）6. 已知a、b、c为常数，点P（a，c）在第二象限，则关于x的方程ax2+bx+c=0根的情况是（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断7. 如图，⊙O的半径为3，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则 的长为（ ）
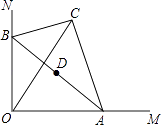
A、π B、 C、2π D、3π8.在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）
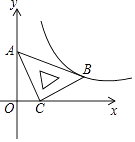A、（ ，0） B、（2，0） C、（ ，0） D、（3，0）二、填空题
-
9. 8的立方根是 ．10. 化简： ÷ = ．11. 分解因式：2a2﹣4a+2= ．12. 如图，直线y=mx+n与抛物线y=ax2+bx+c交于A（﹣1，p），B（4，q）两点，则关于x的不等式mx+n＞ax2+bx+c的解集是 ．
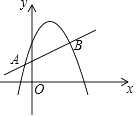13. 小明的爸爸是个“健步走”运动爱好者，他用手机软件记录了某个月（30天）每天健步走的步数，并将记录结果绘制成了如下统计表：步数（万步）
1.1
1.2
1.3
1.4
1.5
天数
3
7
5
12
3
在每天所走的步数这组数据中，众数和中位数分别是 ．
14.如图，点O是矩形纸片ABCD的对称中心，E是BC上一点，将纸片沿AE折叠后，点B恰好与点O重合．若BE=3，则折痕AE的长为 ．
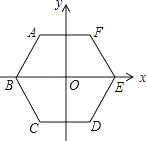
15.如图，边长为4的正六边形ABCDEF的中心与坐标原点O重合，AF∥x轴，将正六边形ABCDEF绕原点O顺时针旋转n次，每次旋转60°．当n=2017时，顶点A的坐标为 ．
16.如图，在Rt△ABC中，BC=2，∠BAC=30°，斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动，下列结论：
①若C、O两点关于AB对称，则OA=2 ；
②C、O两点距离的最大值为4；
③若AB平分CO，则AB⊥CO；
④斜边AB的中点D运动路径的长为 ；
其中正确的是（把你认为正确结论的序号都填上）．
三、解答题
-
17.(1)、计算：|﹣ |﹣ +20170；(2)、解方程： = ．18.
如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC．
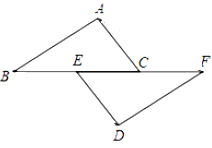(1)、求证：△ABC≌△DFE；
(2)、连接AF、BD，求证：四边形ABDF是平行四边形．19. 咸宁市某中学为了解本校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况，随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图所示的两幅不完整统计图，请你根据图中信息解答下列问题：
(1)、补全条形统计图，“体育”对应扇形的圆心角是度；(2)、根据以上统计分析，估计该校2000名学生中喜爱“娱乐”的有人；(3)、在此次问卷调查中，甲、乙两班分别有2人喜爱新闻节目，若从这4人中随机抽取2人去参加“新闻小记者”培训，请用列表法或画树状图的方法求所抽取的2人来自不同班级的概率．20. 小慧根据学习函数的经验，对函数y=|x﹣1|的图象与性质进行了探究．下面是小慧的探究过程，请补充完整：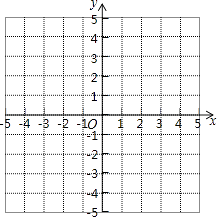
(1)、函数y=|x﹣1|的自变量x的取值范围是；(2)、列表，找出y与x的几组对应值．x
…
﹣1
0
1
2
3
…
y
…
b
1
0
1
2
…
其中，b=；
(3)、在平面直角坐标系xOy中，描出以上表中对对应值为坐标的点，并画出该函数的图象；(4)、写出该函数的一条性质： ．21. 如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点，过点D作DF⊥AC，垂足为点F．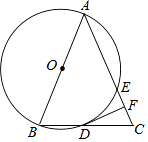
(1)、求证：DF是⊙O的切线；(2)、若AE=4，cosA= ，求DF的长．22. 某公司开发出一款新的节能产品，该产品的成本价为6元/件，该产品在正式投放市场前通过代销点进行了为期一个月（30天）的试营销，售价为8元/件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象，图中的折线ODE表示日销售量y（件）与销售时间x（天）之间的函数关系，已知线段DE表示的函数关系中，时间每增加1天，日销售量减少5件．
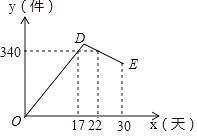(1)、第24天的日销售量是件，日销售利润是元．(2)、求y与x之间的函数关系式，并写出x的取值范围；(3)、日销售利润不低于640元的天数共有多少天？试销售期间，日销售最大利润是多少元？23. 定义：数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称这个三角形为“智慧三角形”．
理解：
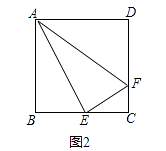
(1)、如图1，已知A、B是⊙O上两点，请在圆上找出满足条件的点C，使△ABC为“智慧三角形”（画出点C的位置，保留作图痕迹）；
(2)、如图2，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF= CD，试判断△AEF是否为“智慧三角形”，并说明理由；运用：
(3)、如图3，在平面直角坐标系xOy中，⊙O的半径为1，点Q是直线y=3上的一点，若在⊙O上存在一点P，使得△OPQ为“智慧三角形”，当其面积取得最小值时，直接写出此时点P的坐标．
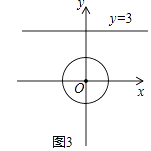24.如图，抛物线y= x2+bx+c与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6．
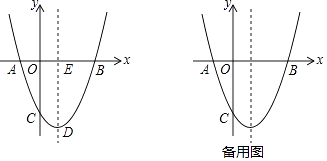(1)、求抛物线的解析式及点D的坐标；(2)、连接BD，F为抛物线上一动点，当∠FAB=∠EDB时，求点F的坐标；(3)、平行于x轴的直线交抛物线于M、N两点，以线段MN为对角线作菱形MPNQ，当点P在x轴上，且PQ= MN时，求菱形对角线MN的长．