2017年甘肃省武威十八中高考数学一模试卷（理科）

试卷更新日期：2017-07-05 类型：高考模拟

进入出卷网下载

一、选择题

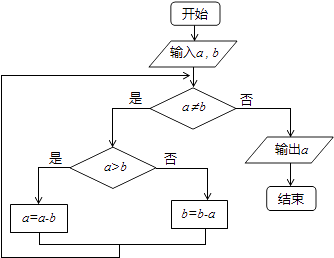
1. 已知集合A={1，2，3}，B={x|（x+1）（x﹣2）＜0，x∈Z}，则A∪B=（）

A、{1} B、{1，2} C、{0，1，2，3} D、{﹣1，0，1，2，3}

查看试题解析
2. 设复数z满足 $\frac{1 + z}{1 - z}$ =i，则|z|=（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
3. 下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（）

A、y= $\frac{1}{x}$ B、y=|x|﹣1 C、y=lg x D、y=（ $\frac{1}{2}$ ）^|^x^|

查看试题解析
4. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（）

A、0 B、2 C、4 D、14

查看试题解析
5. 已知 $c o s (π - α) = \frac{4}{5}$ ，且α为第三象限角，则tan2α的值等于（）

A、 $\frac{3}{4}$ B、﹣ $\frac{3}{4}$ C、 $\frac{24}{7}$ D、﹣ $\frac{24}{7}$

查看试题解析
6. 一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为（）

A、 $\frac{1}{3}$ + $\frac{2}{3}$ π B、 $\frac{1}{3}$ + $\frac{\sqrt{2}}{3}$ π C、 $\frac{1}{3}$ + $\frac{\sqrt{2}}{6}$ π D、1+ $\frac{\sqrt{2}}{6}$ π

查看试题解析
7. 已知实数x，y满足 ${\begin{matrix} y \geq 1 \\ y \leq 2 x - 1 \\ x + y \leq m \end{matrix}$ ，如果目标函数z=x﹣y的最小值为﹣1，则实数m等于（）

A、7 B、5 C、4 D、3

查看试题解析
8. 若等比数列{a_n}的各项均为正数，a₁+2a₂=3，a₃²=4a₂a₆ ，则a₄=（）

A、 $\frac{3}{8}$ B、 $\frac{24}{5}$ C、 $\frac{3}{16}$ D、 $\frac{9}{16}$

查看试题解析
9. 若函数f（x）=sin（ωx﹣ $\frac{π}{6}$ ）（ω＞0）的图象相邻两个对称中心之间的距离为 $\frac{π}{2}$ ，则f（x）的一个单调递增区间为（）

A、（﹣ $\frac{π}{6}$ ， $\frac{π}{3}$ ） B、（﹣ $\frac{π}{3}$ ， $\frac{π}{6}$ ） C、（ $\frac{π}{6}$ ， $\frac{2 π}{3}$ ） D、（ $\frac{π}{3}$ ， $\frac{5 π}{6}$ ）

查看试题解析
10. 过抛物线y²=2px（p＞0）的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A、B两点，则 $\frac{| A F |}{| B F |}$ 的值等于（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
11. 若圆（x﹣3）²+（y+5）²=r²有且只有两个点到直线4x﹣3y=2的距离等于1，则半径r的范围是（）

A、（4，6） B、（4，6] C、[4，6） D、[4，6]

查看试题解析
12. 已知g（x）是定义在R上的奇函数，且当x＜0时，g（x）=﹣ln（1﹣x），函数f（x）= ${\begin{matrix} x^{3} ， x \leq 0 \\ g (x) ， x > 0 \end{matrix}$ ，若f（2﹣x²）＞f（x），则x的取值范围是（）

A、（﹣∞，﹣2）∪（1，+∞） B、（﹣∞，1）∪（2，+∞） C、（﹣2，1） D、（1，2）

查看试题解析

二、填空题

13. 已知m∈R，向量 $\vec{a}$ =（m，1）， $\vec{b}$ =（2，﹣6），且 $\vec{a}$ ⊥ $\vec{b}$ ，则| $\vec{a}$ ﹣ $\vec{b}$ |= ．

查看试题解析
14. 若随机变量ξ～N（2，1），且P（ξ＞3）=0.158 7，则P（ξ＞1）= ．

查看试题解析
15. 如果（3x﹣ $\frac{1}{\sqrt[3]{x^{2}}}$ ）ⁿ的展开式中各项系数之和为128，则展开式中 $\frac{1}{x^{3}}$ 的系数是．

查看试题解析
16. 如图所示，一个圆柱形乒乓球筒，高为20厘米，底面半径为2厘米．球筒的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切（球筒和乒乓球厚度均忽略不计）．一个平面与两个乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，则该椭圆的离心率为．

查看试题解析

三、解答题

17. △ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．
（Ⅰ）求C；
（Ⅱ）若c= $\sqrt{7}$ ，△ABC的面积为 $\frac{3 \sqrt{3}}{2}$ ，求△ABC的周长．

查看试题解析

18. 某校高三共有900名学生，高三模拟考之后，为了了解学生学习情况，用分层抽样方法从中抽出若干学生此次数学成绩，按成绩分组，制成如下的频率分布表：

组号	第一组	第二组	第二组	第四组
分组	[70，80）	[80，90）	[90，100）	[100，110）
频数	6	4	22	20
频率	0.06	0.04	0.22	0.20
组号	第五组	第六组	第七组	第八组
分组	[110，120）	[120，130）	[130，140）	[140，150]
频数	18	a	10	5
频率	b	0.15	0.10	0.05

(1)、若频数的总和为c，试求a，b，c的值；

(2)、为了了解数学成绩在120分以上的学生的心理状态，现决定在第六、七、八组中用分层抽样方法抽取6名学生，在这6名学生中又再随机抽取2名与心理老师面谈，令第七组被抽中的学生数为随机变量ξ，求随机变量ξ的分布列和数学期望；

(3)、估计该校本次考试的数学平均分．

查看试题解析

19.
如图，三棱锥P﹣ABC中，PC⊥平面ABC，PC=3，∠ACB= $\frac{π}{2}$ ．D，E分别为线段AB，BC上的点，且CD=DE= $\sqrt{2}$ ，CE=2EB=2．
（Ⅰ）证明：DE⊥平面PCD
（Ⅱ）求二面角A﹣PD﹣C的余弦值．

查看试题解析
20. 已知焦点在y轴上的椭圆E的中心是原点O，离心率等于 $\frac{\sqrt{3}}{2}$ ，以椭圆E的长轴和短轴为对角线的四边形的周长为4 $\sqrt{5}$ ，直线，l：y=kx+m与y轴交干点P，与椭圆E相交于A、B两个点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若 $\vec{A P}$ =3 $\vec{P B}$ ，求m²的取值范围．

查看试题解析
21. 设函数f（x）=2lnx+ $\frac{1}{x}$ ．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）如果对所有的x≥1，都有f（x）≤ax，求a的取值范围．

查看试题解析
22. 在直角坐标xOy中，直线l的参数方程为{ ${\begin{matrix} x = \frac{\sqrt{2}}{2} t \\ y = 3 + \frac{\sqrt{2}}{2} t \end{matrix}$ （t为参数）在以O为极点．x轴正半轴为极轴的极坐标系中．曲线C的极坐标方程为ρ=4sinθ﹣2cosθ．
（I）求直线l的普通方程与曲线C的直角坐标方程：
（Ⅱ）若直线l与y轴的交点为P，直线l与曲线C的交点为A，B，求|PA||PB|的值．

查看试题解析
23. 设f（x）=|ax﹣1|．
（Ⅰ）若f（x）≤2的解集为[﹣6，2]，求实数a的值；
（Ⅱ）当a=2时，若存在x∈R，使得不等式f（2x+1）﹣f（x﹣1）≤7﹣3m成立，求实数m的取值范围．

查看试题解析