2017年广西南宁市、北海市、钦州市、防城港市中考数学试卷
试卷更新日期:2017-07-05 类型:中考真卷
一、选择题
-
1. 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
 A、100° B、80° C、60° D、40°2. 在下列几何体中,三视图都是圆的为( )A、
A、100° B、80° C、60° D、40°2. 在下列几何体中,三视图都是圆的为( )A、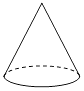 B、
B、 C、
C、 D、
D、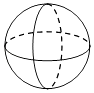 3. 根据习近平总书记在“一带一路”国际合作高峰论坛开幕式上的演讲,中国将在未来3年向参与“一带一路”建设的发展中国家和国际组织提供60000000000元人民币援助,建设更多民生项目,其中数据60 000 000 000用科学记数法表示为( )A、0.6×1010 B、0.6×1011 C、6×1010 D、6×10114. 2017•南宁)下列运算正确的是( )A、﹣3(x﹣4)=﹣3x+12 B、(﹣3x)2•4x2=﹣12x4 C、3x+2x2=5x3 D、x6÷x2=x35. 一元一次不等式组 的解集在数轴上表示为( )A、
3. 根据习近平总书记在“一带一路”国际合作高峰论坛开幕式上的演讲,中国将在未来3年向参与“一带一路”建设的发展中国家和国际组织提供60000000000元人民币援助,建设更多民生项目,其中数据60 000 000 000用科学记数法表示为( )A、0.6×1010 B、0.6×1011 C、6×1010 D、6×10114. 2017•南宁)下列运算正确的是( )A、﹣3(x﹣4)=﹣3x+12 B、(﹣3x)2•4x2=﹣12x4 C、3x+2x2=5x3 D、x6÷x2=x35. 一元一次不等式组 的解集在数轴上表示为( )A、 B、
B、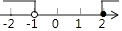 C、
C、 D、
D、 6. 今年世界环境日,某校组织的保护环境为主题的演讲比赛,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是( )A、8.8分,8.8分 B、9.5分,8.9分 C、8.8分,8.9分 D、9.5分,9.0分7. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )
6. 今年世界环境日,某校组织的保护环境为主题的演讲比赛,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是( )A、8.8分,8.8分 B、9.5分,8.9分 C、8.8分,8.9分 D、9.5分,9.0分7. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( ) A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC8. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )A、 B、 C、 D、9. 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长等于( )
A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC8. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )A、 B、 C、 D、9. 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长等于( ) A、 B、 C、 D、10. 一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为vkm/h,则可列方程为( )A、 = B、 = C、 = D、 =11.
A、 B、 C、 D、10. 一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为vkm/h,则可列方程为( )A、 = B、 = C、 = D、 =11.如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
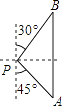 A、60 n mile B、60 n mile C、30 n mile D、30 n mile12. 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y= (x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则 的值为( )
A、60 n mile B、60 n mile C、30 n mile D、30 n mile12. 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y= (x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算:|﹣6|= .14. 红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有85名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有人.15. 已知 是方程组 的解,则3a﹣b= .16. 如图,菱形ABCD的对角线相交于点O,AC=2,BD=2 ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为 .
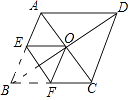 17. 对于函数y= ,当函数值y<﹣1时,自变量x的取值范围是 .18.
17. 对于函数y= ,当函数值y<﹣1时,自变量x的取值范围是 .18.如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为 .

三、解答题
-
19. 计算:﹣(﹣2)+ ﹣2sin45°+(﹣1)3 .20. 先化简,再求值:1﹣ ÷ ,其中x= ﹣1.21.
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
 (1)、把△ABC向上平移3个单位后得到△A1B1C1 , 请画出△A1B1C1并写出点B1的坐标;(2)、已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2 , 并直接写出直线l的函数解析式.22. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)、把△ABC向上平移3个单位后得到△A1B1C1 , 请画出△A1B1C1并写出点B1的坐标;(2)、已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2 , 并直接写出直线l的函数解析式.22. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.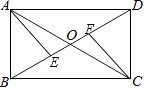 (1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积.23. 为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积.23. 为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题: (1)、在这次调查中,一共调查了名市民,扇形统计图中,C组对应的扇形圆心角是°;(2)、请补全条形统计图;(3)、若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.24. 为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2014年图书借阅总量是7500本,2016年图书借阅总量是10800本.(1)、求该社区的图书借阅总量从2014年至2016年的年平均增长率;(2)、已知2016年该社区居民借阅图书人数有1350人,预计2017年达到1440人,如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长a%,求a的值至少是多少?25. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)、在这次调查中,一共调查了名市民,扇形统计图中,C组对应的扇形圆心角是°;(2)、请补全条形统计图;(3)、若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.24. 为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2014年图书借阅总量是7500本,2016年图书借阅总量是10800本.(1)、求该社区的图书借阅总量从2014年至2016年的年平均增长率;(2)、已知2016年该社区居民借阅图书人数有1350人,预计2017年达到1440人,如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长a%,求a的值至少是多少?25. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.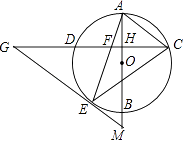 (1)、求证:△ECF∽△GCE;(2)、求证:EG是⊙O的切线;(3)、延长AB交GE的延长线于点M,若tanG= ,AH=3 ,求EM的值.26.
(1)、求证:△ECF∽△GCE;(2)、求证:EG是⊙O的切线;(3)、延长AB交GE的延长线于点M,若tanG= ,AH=3 ,求EM的值.26.如图,已知抛物线y=ax2﹣2 ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
 (1)、直接写出a的值、点A的坐标及抛物线的对称轴;(2)、点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;(3)、证明:当直线l绕点D旋转时, + 均为定值,并求出该定值.
(1)、直接写出a的值、点A的坐标及抛物线的对称轴;(2)、点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;(3)、证明:当直线l绕点D旋转时, + 均为定值,并求出该定值.