2017年广西贵港市中考数学试卷

试卷更新日期：2017-07-05 类型：中考真卷

进入出卷网下载

一、选择题

1. 7的相反数是（）

A、7 B、﹣7 C、 $\frac{1}{7}$ D、﹣ $\frac{1}{7}$

查看试题解析
2. 数据3，2，4，2，5，3，2的中位数和众数分别是（）

A、2，3 B、4，2 C、3，2 D、2，2

查看试题解析
3. 如图是一个空心圆柱体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
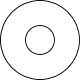4. 下列二次根式中，最简二次根式是（）

A、 $- \sqrt{2}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{5}}$ D、 $\sqrt{a^{2}}$

查看试题解析
5. 下列运算正确的是（）

A、3a²+a=3a³ B、2a³•（﹣a²）=2a⁵ C、4a⁶+2a²=2a³ D、（﹣3a）²﹣a²=8a²

查看试题解析
6. 在平面直角坐标系中，点P（m﹣3，4﹣2m）不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 下列命题中假命题是（）

A、正六边形的外角和等于360° B、位似图形必定相似 C、样本方差越大，数据波动越小 D、方程x²+x+1=0无实数根

查看试题解析
8. 从长为3，5，7，10的四条线段中任意选取三条作为边，能构成三角形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
9. 如图，A，B，C，D是⊙O上的四个点，B是 $\hat{A C}$ 的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（）

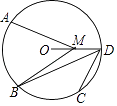A、45° B、60° C、75° D、85°

查看试题解析
10. 将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（）

A、y=（x﹣1）²+1 B、y=（x+1）²+1 C、y=2（x﹣1）²+1 D、y=2（x+1）²+1

查看试题解析
11. 如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（）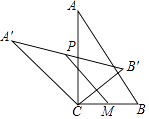

A、4 B、3 C、2 D、1

查看试题解析
12. 如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN²+CM²=MN²；⑤若AB=2，则S_△_OMN的最小值是 $\frac{1}{2}$ ，其中正确结论的个数是（）

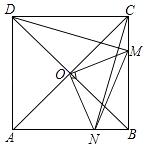A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 计算：﹣3﹣5= ．

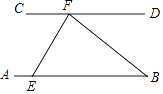
查看试题解析
14. 中国的领水面积约为370 000km² ，将数370 000用科学记数法表示为．

查看试题解析
15. 如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为．

查看试题解析
16. 如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为．

查看试题解析
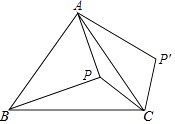17. 如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与 $\hat{A B}$ 交于点D，以O为圆心，OC的长为半径作 $\hat{C E}$ 交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为．（结果保留π）

查看试题解析
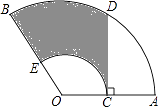18. 如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y= $\frac{k}{x}$ （x＞0）与△ABC总有公共点，则k的取值范围是．

查看试题解析

三、解答题

19. 计算题

(1)、计算：|﹣3|+（ $\sqrt{5}$ +π）⁰﹣（﹣ $\frac{1}{2}$ ）^﹣²﹣2cos60°；

(2)、先化简，在求值：（ $\frac{1}{a - 1}$ ﹣ $\frac{1}{a + 1}$ ）+ $\frac{4 + 2 a}{a^{2} - 1}$ ，其中a=﹣2+ $\sqrt{2}$ ．

查看试题解析
20.
尺规作图（不写作法，保留作图痕迹）：
已知线段a和∠AOB，点M在OB上（如图所示）．

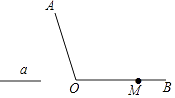(1)、在OA边上作点P，使OP=2a；

(2)、作∠AOB的平分线；

(3)、过点M作OB的垂线．

查看试题解析
21. 如图，一次函数y=2x﹣4的图象与反比例函数y= $\frac{k}{x}$ 的图象交于A，B两点，且点A的横坐标为3．

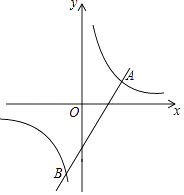(1)、求反比例函数的解析式；

(2)、求点B的坐标．

查看试题解析
22. 在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：
频率分布表
阅读时间
（小时）
频数
（人）
频率
1≤x＜2
18
0.12
2≤x＜3
a
m
3≤x＜4
45
0.3
4≤x＜5
36
n
5≤x＜6
21
0.14
合计
b
1

(1)、填空：a= ， b= ， m= ， n=；

(2)、将频数分布直方图补充完整（画图后请标注相应的频数）；

(3)、若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数．

查看试题解析
23. 某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分，积分超过15分才能获得参赛资格．

(1)、已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；

(2)、如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？

查看试题解析
24. 如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．

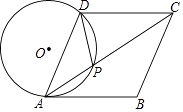(1)、求证：AB是⊙O的切线；

(2)、若AC=8，tan∠BAC= $\frac{\sqrt{2}}{2}$ ，求⊙O的半径．

查看试题解析
25.
如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．

(1)、写出C，D两点的坐标（用含a的式子表示）；

(2)、设S_△_BCD：S_△_ABD=k，求k的值；

(3)、当△BCD是直角三角形时，求对应抛物线的解析式．

查看试题解析
26. 已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD沿BD所在直线折叠，使点A落在点P处．

(1)、
如图1，若点D是AC中点，连接PC．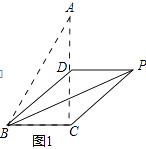
①写出BP，BD的长；
②求证：四边形BCPD是平行四边形．

(2)、
如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．

查看试题解析

阅读时间（小时）	频数（人）	频率
1≤x＜2	18	0.12
2≤x＜3	a	m
3≤x＜4	45	0.3
4≤x＜5	36	n
5≤x＜6	21	0.14
合计	b	1