2019-2020学年初中数学八年级上学期期中模拟试卷（浙教版）
试卷更新日期：2019-10-17 类型：期中考试
一、单选题
-
1. 下列四个标志是关于安全警示的标志，在这些标志中，是轴对称图形的是（ ）A、
当心吊物安全
B、
当心触电安全
C、
当心滑跌安全
D、
注意安全
2. 以下列各组数据为边长作三角形，其中能组成直角三角形的是（ ）A、5，12，13 B、3，5，2 C、6，9，14 D、4，10，133. 通过如下尺规作图，能确定点D是BC边中点的是（ ）A、
B、
C、
D、
4. 《九章算术》是我国古代的数学名著，书中的“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺.问折者高几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？设折断后离地面的高度为x尺，则可列方程为（ ）A、x2–3=（10–x）2 B、x2–32=（10–x）2 C、x2+3=（10–x）2 D、x2+32=（10–x）25. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N为圆心，大于 MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，若CD=3，则BD的长是（ ）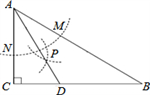
A、7 B、6 C、5 D、46. 已知a、b、c为△ 的三边，且满足 ，则△ 是A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定7. 如图，在 中， ，分别以 、 为圆心，以大于 的长为半径画弧，两弧相交于 、 两点，直线 交 于点 ，若 的周长是12，则 的长为（ ）
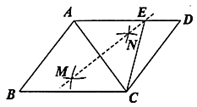A、6 B、7 C、8 D、118. 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC.将仪器上的点A ∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线·此角平分仪的画图原理是：根据仪器结构，可得△ABC △ADC，这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是（ ）
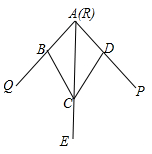A、SAS B、ASA C、AAS D、SSS9. 如图，C，E是直线l两侧的点，以点C为圆心，CE长为半径作圆弧交l于A，B两点；再分别以A，B为圆心，大于 AB的长为半径作圆弧，两弧交于点D，连接CA，CB，CD，下列结论不一定成立的是（ ）
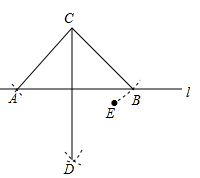A、CD⊥l B、点A，B关于直线CD对称 C、CD平分∠ACB D、点C，D关于直线l对称10. 如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BD=DG.下列结论：（1）DE=DF；（2）∠B=∠DGF； （3）AB＜AF+FG；（4）若△ABD和△ADG的面积分别是50和38，则△DFG的面积是8.其中一定正确的有（ ）
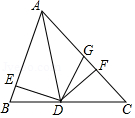A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 命题“两直线平行,同位角相等”的逆命题是。12. 已知 、 、 为 的三边长，且 、 满足 ， 为奇数，则 的周长为.13. 已知，点O为数轴原点，数轴上的A ， B两点分别对应 ， ，以AB为底边作腰长为4的等腰△ABC ， 连接OC ， 以O为圆心，CO长为半径画弧交数轴于点M ， 则点M对应的实数为.14. 在平面直角坐标系中，点 O为坐标原点，A（4，3），B（4，0），在坐标轴上有一点C，使得△AOB 与△COB 全等，则 C 点坐标为.15. 等腰△ABC中，BD⊥AC，垂足为点D，且BD= AC，则等腰△ABC底角的度数为 ．16. 如图①，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成.若直角三角形一个锐角为30°，将各三角形较短的直角边分别向外延长一倍，得到图②所示的“数学风车”设AB＝a，则图中阴影部分面积为(用含a的代数式表示)
三、解答题
-
17. 如图，有一池塘 要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C ， 连接AC并延长到D ， 使 连接BC并延长到E ， 使 连接DE ， 那么量出DE的长，就是A、B的距离 请说明DE的长就是A、B的距离的理由.
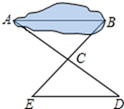18. 已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．
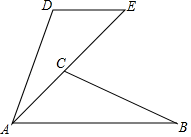19. 图①、图②都是4×4的正方形网格，每个小正方形的顶点为格点，每个小正方形的边长均为1．在图①、图②中已画出线段AB，点A、B均在格点上按下列要求画图：
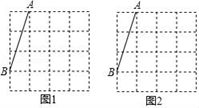(1)、在图①中，以格点为顶点，AB为腰，画一个三边长都是无理数的等腰三角形；(2)、在图②中，以格点为顶点，AB为底的等腰三角形．20. A，B两所学校在一条东西走向公路的同旁，以公路所在直线为x轴建立如图所示的平面直角坐标系，且点A的坐标是(2，2)，点B的坐标是(7， 3)，根据下列要求作图（保留作图痕迹，不用写作法）.
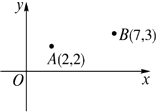(1)、一辆汽车由西向东行驶，在行驶过程中是否存在一点C，使C点到A，B两校的距离相等？如果有，请用尺规作图找出该点；(2)、若在公路边建一游乐场P，使游乐场到两校距离之和最小，通过作图在图中找出建游乐场P的位置，P点的坐标为.21. △ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图（1），根据勾股定理，则a2+b2=c2 ， 若△ABC不是直角三角形，如图（2）和图（3），请你类比勾股定理，试猜想a2+b2与c2的关系，并证明你的结论.
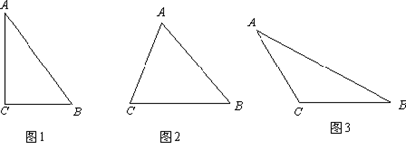22. 如图，在△ABC中，AD⊥BC，垂足为点D，BE⊥AC，垂足为点E，M为AB边的中点，连接ME，MD，ED.
(1)、求证：△MED为等腰三角形；(2)、求证：∠EMD=2∠DAC.23. 如图，在△ABC中，∠BAC=∠ABC，点P在AB上，如果AD⊥CP，BE⊥CP的延长线，垂足分别为D，E，且BE=CD.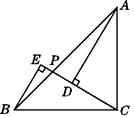
(1)、试探求这个图形中还有哪些相等的线段，并给出证明；(2)、试确定△ABC的形状.24. 如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动(点P和点C，D不重合，点P，A，B不在同一条直线上)，若记∠DAP，∠APB，∠PBC分别为∠α，∠β，∠γ。
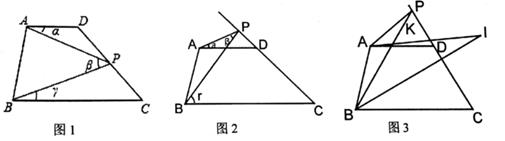(1)、如图1，当点P在线段CD上运动时，写出∠α，∠β，∠γ之间的关系并说出理由；(2)、如图2，如果点P在线段CD的延长线上运动，探究∠α，∠β，∠γ之间的关系，并说明理由。(3)、如图3，BI平分∠PBC，AI交BI于点I，交BP于点K，且∠PAI：∠DAI=5：1，∠APB=20°，∠I=30°，求∠PAI的度数。