2017年四川省南充市中考数学试卷

试卷更新日期：2017-07-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 如果a+3=0，那么a的值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 如图由7个小正方体组合而成的几何体，它的主视图是（）

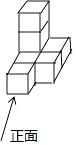A、 B、 C、 D、

查看试题解析
3. 据统计，参加南充市2016年高中阶段学校招生考试的人数为55354人，这个数用科学记数法表示为（）

A、0.55354×10⁵人 B、5.5354×10⁵人 C、5.5354×10⁴人 D、55.354×10³人

查看试题解析
4. 如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（）

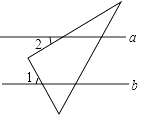A、30° B、32° C、42° D、58°

查看试题解析
5. 下列计算正确的是（）

A、a⁸÷a⁴=a² B、（2a²）³=6a⁶ C、3a³﹣2a²=a D、3a（1﹣a）=3a﹣3a²

查看试题解析
6. 某校数学兴趣小组在一次数学课外活动中，随机抽查该校10名同学参加今年初中学业水平考试的体育成绩，得到结果如下表所示：
成绩/分
36
37
38
39
40
人数/人
1
2
1
4
2
下列说法正确的是（）

A、这10名同学体育成绩的中位数为38分 B、这10名同学体育成绩的平均数为38分 C、这10名同学体育成绩的众数为39分 D、这10名同学体育成绩的方差为2

查看试题解析
7.
如图，等边△OAB的边长为2，则点B的坐标为（）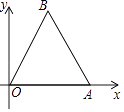

A、（1，1） B、（ $\sqrt{3}$ ，1） C、（ $\sqrt{3}$ ， $\sqrt{3}$ ） D、（1， $\sqrt{3}$ ）

查看试题解析
8. 如图，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为（）

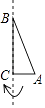A、60πcm² B、65πcm² C、120πcm² D、130πcm²

查看试题解析
9. 已知菱形的周长为4 $\sqrt{5}$ ，两条对角线的和为6，则菱形的面积为（）

A、2 B、 $\sqrt{5}$ C、3 D、4

查看试题解析
10. 二次函数y=ax²+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（）

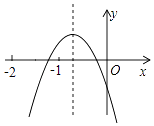A、4ac＜b² B、abc＜0 C、b+c＞3a D、a＜b

查看试题解析

二、填空题

11. 如果 $\frac{1}{m - 1}$ =1，那么m= ．

查看试题解析
12. 计算：|1﹣ $\sqrt{5}$ |+（π﹣ $\sqrt{3}$ ）⁰= ．

查看试题解析
13. 经过某十字路口的汽车，可直行，也可向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过该十字路口时都直行的概率是．

查看试题解析
14. 如图，在▱ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，且CG=2BG，S_△_BPG=1，则S_▱AEPH= ．

查看试题解析
15. 小明从家到图书馆看报然后返回，他离家的距离y与离家的时间x之间的对应关系如图所示，如果小明在图书馆看报30分钟，那么他离家50分钟时离家的距离为 km．

查看试题解析
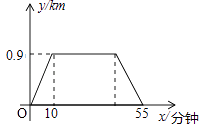16.
如图，正方形ABCD和正方形CEFG边长分别为a和b，正方形CEFG绕点C旋转，给出下列结论：①BE=DG；②BE⊥DG；③DE²+BG²=2a²+b² ，其中正确结论是（填序号）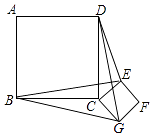

查看试题解析

三、解答题

17. 化简（1﹣ $\frac{x}{x^{2} + x}$ ）÷ $\frac{x - 1}{x + 1}$ ，再任取一个你喜欢的数代入求值．

查看试题解析
18. 在“宏扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如下：

(1)、如图，希望参加活动C占20%，希望参加活动B占15%，则被调查的总人数为人，扇形统计图中，希望参加活动D所占圆心角为度，根据题中信息补全条形统计图．

(2)、学校现有800名学生，请根据图中信息，估算全校学生希望参加活动A有多少人？

查看试题解析
19. 如图，DE⊥AB，CF⊥AB，垂足分别是点E、F，DE=CF，AE=BF，求证：AC∥BD．

查看试题解析
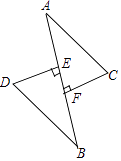20. 已知关于x的一元二次方程x²﹣（m﹣3）x﹣m=0

(1)、求证：方程有两个不相等的实数根；

(2)、如果方程的两实根为x₁、x₂ ，且x₁²+x₂²﹣x₁x₂=7，求m的值．

查看试题解析
21. 如图，直线y=kx（k为常数，k≠0）与双曲线y= $\frac{m}{x}$ （m为常数，m＞0）的交点为A、B，AC⊥x轴于点C，∠AOC=30°，OA=2

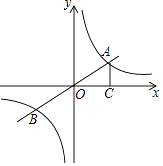(1)、求m、k的值；

(2)、点P在y轴上，如果S_△_ABP=3k，求P点的坐标．

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F．

(1)、求证：DE是⊙O的切线；

(2)、若CF=2，DF=4，求⊙O直径的长．

查看试题解析
23. 学校准备租用一批汽车，现有甲、乙两种大客车，甲种客车每辆载客量45人，乙种客车每辆载客量30人，已知1辆甲种客车和3辆乙种客车共需租金1240元，3辆甲种客车和2辆乙种客车共需租金1760元．

(1)、求1辆甲种客车和1辆乙种客车的租金分别是多少元？

(2)、学校计划租用甲、乙两种客车共8辆，送330名师生集体外出活动，最节省的租车费用是多少？

查看试题解析
24.
如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF= $\frac{1}{4}$ AB．

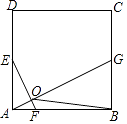(1)、求证：EF⊥AG；

(2)、若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？

(3)、正方形ABCD的边长为4，P是正方形ABCD内一点，当S_△_PAB=S_△_OAB ，求△PAB周长的最小值．

查看试题解析
25.
如图1，已知二次函数y=ax²+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣ $\frac{8}{3}$ ，直线l的解析式为y=x．

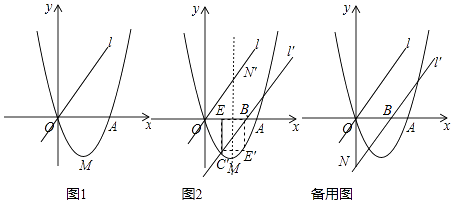(1)、求二次函数的解析式；

(2)、直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；

(3)、在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．

查看试题解析

成绩/分	36	37	38	39	40
人数/人	1	2	1	4	2